OPOWIEŚĆ KOSMOLOGICZNA

autor: Janusz Bator

Część I

Fundamenty tej Opowieści

Spis treści podrozdziałów

Tytuły są podlinkowane. Wystarczy kliknąć, aby przenieść się bezpośrednio do wybranego podrozdziału.

1.1 Fundamenty fundamentów.

1.2. System liczb i miar Wszechświata.

1.3. Czas i rzeczywistość, czyli „pragma”.

1.4. Przestrzeń i nadprzestrzeń. Kwanty przestrzeni, czyli spacjony.

1.5. Geometrie przestrzeni.

1.6. Grawitacja dodatnia i ujemna. Ładunki grawitacji.

1.7 Składniki Wszechświata.

1.8 Intropia.

1.9. O pewnym oddziaływaniu grawitacyjnym, odpowiedzialnym za ekspansję Wszechświata.

1.10 Bezmasowy foton to fikcja.

1.1 Fundamenty fundamentów.

NIST Reference on Constants, Units and Uncertainty. Zbiór wartości liczbowych dotyczących wszystkich zdefiniowanych i potwierdzonych pomiarami wielkości fizycznych, zgrupowanych w 10 działach. Bardzo istotną cechą tego zbioru jest zamieszczenie standardowych niepewności pomiarów (standard uncertainty) i względnych niepewności pomiarów (relative standard uncertainty).

Tabele NIST (National Institute of Standards and Technology) oraz CODATA (Commitee on Data for Science and Technology), okresowo uaktualniane, są wspaniałym osiągnięciem nauki, pozwalającym na porównywanie wartości uzyskiwanych z obliczeń lub pomiarów z wartościami ustalonymi przez najbardziej autorytatywny międzynarodowy organ naukowy.

Odwołując się do tych tabel, będę stosował akronim CODATA.

Niestety w tym fundamencie jest pewien szczególny wyjątek, coś jakby niestandardowa cegła w murze, a mianowicie „szybkość światła w próżni”. Obok ogólnie znanej i stosowanej wartości 299 799 458 m/s, zamiast zakresu niepewności (a przecież podana wartość sugeruje względną dokładność pomiaru 10^-8) zamieszczono słowo exact, co nasuwa podejrzenie, że szybkość światła, uznana jako stała fizyczna „c”, została ostatecznie ustalona arbitralnie. Poza tym „exact” nie bardzo licuje z misją nauki jako procesu nieustannego dochodzenia do prawdy. Tak na serio, co można opatrzyć atrybutem exact?

W tej Opowieści sprawa ta jest na tyle ważna, że rozwinę ją w jednym z następnych rozdziałów.

Wczesne raporty ESA (Europen Space Agency) po 9 miesiącach misji satelity Planck, zostały ogłoszone na pamiętnej (dla mnie) konferencji prasowej ESA w Paryżu w dniu 21 marca 2013 r. Pomimo wyrażonych tam opinii, że przedstawione wyniki nie są sprzeczne z „obowiązującym” modelem kosmologicznym Lambda CDM, trudno było nie odnosić wrażenia, że właśnie ten oto model zaczyna się chwiać w posadach, co być może skłoni teoretyków kosmologii do poważnej jego rewizji.

Po wspomnianej konferencji nastąpiła lawina szczegółowych raportów ESA pod zbiorowym tytułem ESA Planck Publications. Dla mnie najważniejszymi okazały się publikacje z mapami kosmicznego mikrofalowego promieniowania tła (CMB), a zwłaszcza te, które zawierały mapy i komentarze dotyczące szumów nałożonych na CMB. Planck był pierwszym satelitą, który z dużą dokładnością i wiarygodnością dostarczył informacji o „jeszcze jednym poziomie promieniowania” tła, czyli warstwie chaotycznych szumów. Czyżby miałoby to być poszukiwane „promieniowanie Hawkinga”?

Najbardziej pomocne były dla mnie m.in. następujące publikacje, mające w tym czasie status preprintów Uniwersytetu Cornella:

arXiv:1303.5086v1 (22.02.2013), pt. Planck 2013 results. XXVI. Background geometry and topology of theUniverse,

oraz

1303.5063,v.3 (astr-ph.IM, 2 Febr. 1014) pt. Planck 2013 results. II. Low Frequency Instrument data processing

Kwestionowanie niektórych twierdzeń i przewidywań współczesnej teorii Wielkiego Wybuchu i wielkiej inflacji, jak:

- „brak” we Wszechświecie obecności tzw. antymaterii oraz monopoli magnetycznych, wyemitowanych w Wielkim Wybuchu w dokładnie takich samych ilościach energii (masy),

- istnienie „ciemnych” składników Wszechświata w rodzaju „ciemnej materii” i „ciemnej energii”,

- nieustanne rozszerzanie się Wszechświata, na co prawo Hubble’a miałoby być wystarczającym dowodem, a także istnienie „wiecznej inflacji”,

- celowość wysiłków i ponoszenia potrzebnych gdzie indziej kosztów, mających na celu znalezienie bezkonfliktowego styku między fizyką klasyczną i fizyką kwantową, a tym samym celowość wysiłków na rzecz znalezienia tzw. „teorii wszystkiego”.

Mógłbym wymienić jeszcze sporo podobnych przykładów kwestionowania ustaleń naukowych, one same ukażą się w toku dalszego wywodu. Nie pozostawiam jednak wątpliwości, że prawo zachowania energii i informacji pozostają dla mnie nienaruszalne i pankosmiczne.

Zdecydowanie odżegnuję się od jawnego lub skrywanego powoływania się na logikę kreacjonizmu, w celu „wyjaśnienia” zagadek naukowych, jednakże z następującą uwagą:

Nie utożsamiam i nie kojarzę ze sobą poglądów kreacjonistycznych z poglądami tych, którzy wyznając sprawczość „alternatywnego” świata metafizycznego, odwołują się do fenomenu „Objawienia” lub (mającego słabszy kontekst religijny) „natchnienia”. Wyrażam jednak dystans wobec przymiotnika „alternatywnego”. Rozum i objawienie lub natchnienie nie muszą być ze sobą w opozycji, jeśli tylko zostaną uwolnione od doktrynerstwa ideologicznego, zwłaszcza religijnego, albo licytowania się, kto jest bardziej rygorystycznym ateistą. Od czasu narodzin psychologii głębi Freuda i Junga uznaje się wielkie znaczenie „nieświadomości” w postępowaniu człowieka. C.G. Jung, wprowadzając pojęcie archetypu, nie nadawał jednak nieświadomości kontekstu religijnego. Wprowadził także i uzasadnił znaczenie pojęć: percepcja i intuicja, jako funkcji, które mogą wspomagać myślenie i działania czysto rozumowe („racjonalistyczne”).

Warto przy tej okazji przypomnieć polskiego logika i filozofa Jana Łukasiewicza (1879–1956), który jest autorem tzw. logiki trójwartościowej. Oprócz pojęć „prawda” i „fałsz” zaproponował on trzecie: „możliwość” [por. książkę mojego przyjaciela od czasów szkolnych, biologa, onkologa, genetyka filozofa prof. dra. Andrzeja Bomirskiego (1934–2012), Rozmowy o rozumie, wolności i nie tylko. Wydawnictwo Adam Marszałek, Toruń, 2012]. Spory naukowe na ten temat trwają do dzisiaj.

Jest czymś bardzo pociągającym zastąpienie pojęć „rozum” „objawienie/natchnienie” (również „intuicja”) jakimś jednym wspólnym dodatkowym terminem. Coś jakby „rozum i metafizyka człowieka myślącego” w formie zintegrowanej. Wszakże zawsze będziemy mieli wątpliwości co do wiarygodności źródła naszych informacji oraz słuszności naszych konstatacji, co jest przecież jedną z podstawowych zasad nauki. Deklarowanie się z góry po stronie rygorystycznego racjonalizmu lub idealizmu albo, co gorsza, interpretowanie wyników badań eksperymentalnych na tej podstawie wydaje się zbędne i niesprzyjające dyskursowi naukowemu.

1.2 System liczb i miar Wszechświata.

Mówienie lub pisanie, że „Wszechświat jest matematyczny” budzi wątpliwości, nie wiadomo przecież, jakim systemem (lub systemami) matematyki i jakimi algorytmami ten wielki Byt się z natury swojej „posługuje”. W ślad za takimi błyskotliwymi powiedzeniami stworzona została ogromna dziedzina „ziemskiej matematyki kosmologicznej”, niezmiernie wyrafinowanej, którą tak naprawdę rozumie już tylko część uczonych kosmologów-matematyków. Nic dziwnego, że my, Ziemianie, posługujemy się systemami liczbowymi wynikającymi z faktu, że zostaliśmy obdarzeni 10 palcami oraz parami różnych innych organów. Stąd takie rozpowszechnienie systemu dziesiętnego i jego pochodnych, zwłaszcza dwójkowego.

Wszechświaty, jakiekolwiek by były, nie mogą posługiwać się systemami „ziemskimi” m.in. z bardzo oczywistego powodu: nie znają ziemskich pojęć „zero” i „jedność”, a więc również „nieskończoność”, które by były niezbędne do zdefiniowania jakichś bytów. Trzeba pogodzić się z tym, że wszechświaty, a przynajmniej „nasz” Wszechświat, podlegają przede wszystkim prawom fizyki kwantowej, a być może także „subkwantowej”. Nie ma tam, jak mniemam, miejsca na coś takiego, jak ABSOLUTNE NIC („zero”) i ABSOLUTNA PEŁNIA („jedność”), bo takie stany kwantowe nie występują. Słynne pytanie Leibniza w Monadologii trzeba więc uznać po prostu za zgrabną i refleksyjną prowokację filozoficzną, która nadal bywa przedmiotem dociekań naukowych (por. między innymi: Jacek Wojtysiak „Dlaczego istnieje raczej coś niż nic”. 473 stron. Tow. Naukowe KUL. Lublin 2008)

Kosmologiczny system liczbowy zawiera jedynie cztery cyfry. Dwie z nich oznaczane są literami greckimi: Ф (duże fi) i π (małe lub niekiedy duże pi), a symbole pozostałych dwóch są dobrze znane w systemie ziemskim: są to e oraz 1 ( jedynka).

Wspólną cechą tych kosmologicznych cyfr („kosmocyfr”) jest to, że wprawdzie dają się przełożyć na ziemski system liczbowy, ale wtedy okazuje się, że wszystkie są liczbami, a nie cyframi, w dodatku niewymiernymi, a nawet (poza jednym przypadkiem) nieokresowymi. Jeżeli będę je jednak nazywał liczbami, będzie to oznaczać, że mam na myśli kosmocyfry”; chcę bowiem uniknąć nieporozumień, których przyczyną może być używanie terminu „cyfra” w podwójnym znaczeniu.

Liczba Ф jest dodatnim pierwiastkiem równania kwadratowego:

i wynosi:

1,6180339887…

(W większości obliczeń będę ograniczał ich dokładność do sześciu miejsc po przecinku. W uzasadnionych wypadkach do ośmiu miejsc. Wydaje się to wystarczające, a poza tym takie możliwości daje mi mój kalkulator naukowy). Powinna być znana uczniom szkół średnich, jako tzw. liczba złotego podziału odcinka. Mnie akurat tego uczono.

Liczby: π=3,14159265…i e=2,71828183 są również dobrze znane absolwentom szkół średnich. Może jednak być przydatna bliższa znajomość z liczbą e. Otóż liczba ta, występująca także pod nazwą liczby Eulera, jest granicą ciągu liczb według następującego wzoru: e=lim (1+1/n)ⁿ przy n dążącym do nieskończoności. Wielkie znaczenie tej liczby wynika także stąd, że jest ona podstawą logarytmu naturalnego. Ta liczba/cyfra odgrywa bardzo znaczącą rolę w wielu dziedzinach nauki, w których wykazuje uniwersalne właściwości mogące sugerować jej kosmologiczne konotacje.

Z jedynką sprawa jest trochę bardziej złożona. Zgodnie z tym, co napisałem wcześniej, nie występuje w matematyce kosmicznej w swoim ziemskim znaczeniu, ponieważ wyraża jedynie wartość prawdopodobieństwa, z jaką dane nam jest, w określonych warunkach, zbliżyć się do jedynki „absolutnej”, czyli „całości”. W związku z tym może ona przyjmować dwie postaci rozróżnione górnymi prawymi indeksami plus lub minus:

a) jako niedomiarowa:

albo

b) jako nadmiarowa:

gdzie n i m są liczbami naturalnymi i oznaczają w skrótowej notacji krotność powtórzenia pierwszej cyfry po przecinku i tym samym określają dokładność wybraną arbitralnie przez dokonującego obliczeń. Tego typu skrótowe notacje nie są stosowane w znanej mi literaturze i używam ich z konieczności.

Obie jedynki będę niekiedy nazywać „kosmologicznymi”.

W większości obliczeń nie będzie miało większego znaczenia, w jakiej postaci (nadmiarowej lub niedomiarowej) została użyta jedynka i wtedy górne indeksy + i – będą pomijane. W każdym jednak wypadku trzeba pamiętać, że te jedynki nie będą wartościami absolutnymi, lecz probabilistycznymi bądź przybliżonymi.

Pytanie: czy w ogóle coś takiego jak „jedynka absolutna” istnieje? Istnieje, ale jako pojęcie filozoficzne, do którego jeszcze wrócimy w końcowych rozdziałach.

Można także, w analogii do jedynek kosmologicznych, proponować jeszcze „zero kosmologiczne”, czyli wartość asymptotycznie zmierzającą do wirtualnego „zera absolutnego”, ale nigdy tego zera nie osiągającą. Zapis takiego „zera” (tylko nadmiarowego) byłby następujący:

Liczby bardzo małe mogą być jednak wyrażone „kosmologicznie” przez Φ do potęgi (-n). Zapis niedomiarowy zera nie istnieje, bo oznaczałby w ziemskim rozumieniu liczbę ujemną, a powiedzieliśmy, że arytmetyka liczb ujemnych w systemie kosmicznym nie istnieje. Pojęcia „dodatniości” albo „ujemności” będą stosowane jedynie w rozważaniach na gruncie fizyki klasycznej, np. ładunek elektryczny dodatni lub ujemny oraz wszędzie tam, gdzie mamy do czynienia z wielkościami występującymi parami i zależy nam na zaznaczeniu ich przeciwstawności fizycznej. Atrybuty te mają zazwyczaj charakter umowny i są ustalone przez tradycję.

Nie może więc być także jedynki podzielonej przez zero, czyli „nieskończoności”, traktowanej niekiedy przez „ziemskich” matematyków jako zwykła liczba, a nawet cyfra. Skutkuje to również brakiem w Przyrodzie tzw. „osobliwości”, czegoś, co zrosło się z nauką o czarnych dziurach.

System uznaje znane nam działania arytmetyczne: mnożenie, dzielenie, potęgowanie, pierwiastkowanie, logarytmowanie o podstawie Φ, natomiast dodawanie i odejmowanie na zasadach algebry Boole’a w geometrii brył.

Ale to w praktyce matematyki „ziemskiej” nie jest wcale tak proste. Pokażę to na przykładzie podstawowej jednostki długości (w tzw. systemie jednostek naturalnych albo jednostek Plancka), zwanej długością Plancka, oznaczanej literą l z dolnym indeksem małe p, czyli lp. W międzynarodowym systemie jednostek SI, według danych CODATA (2018), długość ta wynosi:

Liczba w nawiasach, zgodnie z zasadami NIST/CODATA, oznacza zakres niepewności ostatnich dwóch cyfr. W tym wypadku wynosi on:

Przekształcenie podanej wartości na liczbę potęgową o podstawie Φ nie sprawia trudności, wystarczy wykonać następujące działanie arytmetyki podstawowej:

Wykładnik potęgowy poszukiwanej liczby o podstawie Φ wyniesie:

Nie cieszmy się przedwcześnie, otrzymana liczba

nie jest zapisem w „czystym” systemie liczbowym Wszechświata, który nazwałem już kosmologicznym. Wszechświat nie zrozumie takiego wykładnika potęgowego, ponieważ ten wykładnik jest liczbą z systemu dziesiętnego. Jego zamiana na liczbę w „czystym” systemie kosmicznym (czyli operującym tylko cyframi kosmicznymi Φ,π,e,1) jest w operacjach algebraicznych bardzo kłopotliwa i często prowadzi do pomyłek, a to m.in. z tego powodu, że często przybiera postać „łańcuchową”, choć trafniejszym określeniem byłoby użycie słowa piramida. W postaci potęgowej na ogół wyglądałoby to tak:

Przy tego rodzaju obliczeniach warto przypominać sobie, że wykładniki liczb potęgowych są bezwymiarowe, jednostki wymiarowe odnoszą się do podstawy. W pokazanym przykładzie postaci łańcuchowej tą podstawą jest najniższa i zarazem graficznie największa liczba/cyfra Φ. Ponadto trzeba pamiętać, że przy transformacji takiej postaci na postać dziesiętną obliczenia kalkulatorowe należy zaczynać od szczytu łańcucha. Przy dużej liczbie ogniw (albo pięter) i wymaganej dużej dokładności zazwyczaj trzeba całe obliczenie wykonać w kilku etapach, bo kalkulator może odmawiać posłuszeństwa tak wysokim wymaganiom i zacząć przekłamywać wyniki.

Na pocieszenie mam dobrą wiadomość: w większości obliczeń, które znajdą się w tej opowieści, liczby potęgowe o podstawie Φ, ale z wykładnikiem dziesiętnym, w operacjach mnożenia, potęgowania, dzielenia, pierwiastkowania i logarytmowania dziesiętnego i naturalnego z innymi liczbami, także o podstawie Φ, są dopuszczalne. Będzie to w istocie zastosowanie bardzo uproszczonego systemu kosmologicznego. Mam uzasadnione obawy, że konsekwentne użycie systemu kosmologicznego pociągnęłoby za sobą okazje do błędów obliczeniowych, zupełnie niepotrzebnie, bo nie miałoby wpływu na kształt tworzonych modeli graficznych, a jedynie na wartości wymiarów, które w tej opowieści nie mają znaczenia, ponieważ będą nas interesować wartości względne.

Akceptacja domniemywanego tutaj systemu liczbowego Wszechświata oznacza w praktyce zerwanie z utrwalonymi od wieków zasadami matematyki przy rozważaniu różnych jego modeli. Proszę jednak, żeby nie zrażać się z tego powodu do dalszej lektury, może się okazać, że ten system jest łatwiejszy do zrozumienia niż ten utrwalony i sprawdzony na Ziemi i w „bliskim Kosmosie”.

W powyższych rozważaniach nie napisałem niczego o kosmologicznym systemie miar. Tu sprawa jest prostsza, bo taki system w kosmologii ziemskiej istnieje niemal od 100 lat, znany jako „System jednostek naturalnych” albo częściej jako „System jednostek Plancka”. Maks Planck zaproponował go w 1899 roku i byłoby zbędne wyjaśnianie istoty systemu tutaj, skoro liczne opisy dostępne są z łatwością np. w Wikipedii i (mam nadzieję) w podręcznikach fizyki dla liceów. Wystarczy, że napiszę, że Planck wywiódł system tylko z czterech stałych fizycznych, które ze swojej definicji mają charakter uniwersalny, a więc kosmiczny. Są to: szybkość światła w próżni „c”, stała grawitacyjna „G”, zredukowana stała Plancka „h przekreślone poziomą kreską” i stała Boltzmanna „k” .

Niestety, nie unikniemy jednak pewnego kłopotu: chodzi o miary kątów. Na ogół nauczono nas w szkole dwóch systemów miar kątów: systemu stopniowego i systemu łukowego. Jednostką systemu „stopniowego” jest stopień, czyli 1/360 część kąta pełnego. Jednostką systemu łukowego jest radian. Są jeszcze inne systemy ziemskie, wymyślone dla konkretnych zastosowań, np. dla artylerii.

Kłopot, o którym wspomniałem, polega na tym, że Wszechświat nie rozumie, co to znaczy np. kąt równy 90 stopni. Nic dziwnego, a czy my sami wiemy, dlaczego kąt prosty to 90 stopni, a nie np. 100 lub 1000? Coś musimy z tym zrobić, ale co?

Na szczęście Wszechświat rozumie, co to znaczy π radianów, a my wiemy, że to oznacza kąt równy 180 stopni. To już wprawdzie coś, ale na tym niestety kończy się edukacja Wszechświata. Wniosek może być radykalny: w systemie miar kątów Wszechświat ma do czynienia tylko z określonymi wartościami tych kątów, żadnymi innymi. Jakie to wartości? Jedną już znamy, to π (oczywiście radianów), a inne to:

π x Φ (pi razy fi, czyli 291,25 stopni), π x Φ² (czyli 471,25 stopni), π x Φ^-1 (czyli 111,25 stopi), π x Φ^-2 (czyli 68,75 stopni) itd.

Dopuszczalne wartości kątów łatwo sobie obliczyć. Uzasadnionym wyjątkiem w tej galerii okazuje się kąt pełny, 360 stopni, którego zapis kosmologiczny byłby następujący:

360 stopni = 2π radianów = (Φ² – Φ^-1) x π

Czy tak jest istotnie w kosmicznej pragmie? Dalsze rozważania w tej opowieści, zwłaszcza dotyczące graficznego modelowania Wszechświata, zdają się potwierdzać powyższe założenie. Wątpliwości zawsze są, ale pamiętajmy, tytuł tej książki to tylko hipoteza, i to nie „naukowa hipoteza”.

1.3 Czas i rzeczywistość czyli „pragma”.

W rozdziale 2.3 napisałem, że w moim mniemaniu nie ma „łagodnego” przejścia między fizyką klasyczną i kwantową, co pociąga za sobą konieczność określania się na jakim gruncie teoretycznym rozważa się jakiś problem fizyki, klasycznym czy kwantowym. W tym pierwszym wypadku oznacza to, że badacz uznaje się za obserwatora zewnętrznego, niemającego z badanym bytem organicznego związku, poza „rozumowym”, logicznym, lecz tylko domniemywanym.

Kosmolog klasyczny nie jest częścią badanego przezeń wszechświata, lecz jego „zewnętrznym” obserwatorem (zakładam w tym miejscu, że istnieje coś takiego jak zewnętrze Wszechświata zamkniętego).

Kosmolog kwantowy wyraża natomiast swoje opinie, jakby sam był zbiorem cząstek i skwantowaną energią, które stanowią integralną część badanego Wszechświata. To nie jest łatwe i raczej teoretyczne. Dla nieprofesjonalnego amatora takie rozszczepienia tożsamości mogą być ryzykowne, zwłaszcza gdy są długotrwałe.

Konsekwencje rozróżnienia pozycji obserwatora są bardzo ważne. W sytuacji „obserwatora kwantowego” nie występują pojęcia takie, jak: ruch, szybkość, moment pędu, przyśpieszenie i wiele innych, postrzeganych za pomocą zmysłów i będących konsekwencją uznania czasu klasycznego, bo taki czas dla „obserwatora kwantowego” nie istnieje. Istnieje tylko chwila „teraz”. Jeżeli coś się dzieje, to znaczy, że to „coś” właśnie staje się ogniwem w łańcuchu przyczynowo-skutkowym, w którym zarówno przyczyna, jak i skutek wyrażane są liczbowo, jako prawdopodobieństwa ich zaistnienia. Zamiast ruchu mamy do czynienia ze stawaniem się w niezwykle krótkim momencie skwantowanego czasu. Dla ułatwienia wyobraźni (i tylko dlatego) możemy założyć, że w naszym Wszechświecie ten moment ma wymiar najkrótszego odcinka czasu, mającego zdaniem nauki sens fizyczny, czyli czasu Plancka, i jest rzędu 10^-43 sekundy. Te „momenty” nie układają się w znaną klasyczną oś czasu, ponieważ kolejne ogniwa łańcucha są jedynie prawdopodobieństwami lub raczej „chmurkami prawdopodobieństw” o różnej gęstości. Powstaje przy tym uzasadnione domniemanie, że Wszechświat funkcjonuje według taktującego zegara o częstotliwości 1/2 t_p,gdzie t_p oznacza czas Plancka, czyli oscylator o częstotliwości rzędu 10⁴³Hz. Ogólna teoria względności (OTW) ma swój ogromny sens jedynie w fizyce i kosmologii klasycznej. Sformułowanie relatywistyczna teoria kwantowa może być uznane jako wewnętrznie sprzeczne.

Nie uciekniemy jednak od fizyki klasycznej, a więc i od czasu, ponieważ z natury interesuje nas proces, który nazywamy ewolucją Wszechświata, co nie jest możliwe bez klasycznego pojęcia czasu. Tak też będzie w przedstawianej tu hipotezie: obrazy graficzne będą przedstawiać to, co mógłby postrzegać obserwator klasyczny, ale na podstawie poprzedzających usiłowań wyobrażenia sobie tego, co mógłby postrzegać obserwator kwantowy.

Czas klasyczny, wyobrażany graficznie jako prosta, krzywa, okrąg i inne figury jednowymiarowe, ze strzałkami wskazującymi kierunki upływu, jest wymysłem nas, Ziemian, ponieważ wszystko dokoła widzimy jako śmiertelne, mające swój początek i kres. Nie można jednak, tylko dla ułatwienia wyobraźni, przypisywać ziemskich wyobrażeń obserwowanym obiektom kosmicznym. Niektórzy fizycy, nawet ci uznani za „wybitnych”, posuwają się niekiedy nawet do tego, że sugerują możliwość odtworzenia odwrotnego upływu czasu, posługując się filmem prezentowanym od końca, co jest oczywiście mylące. Taki film o odwróconym łańcuchu przyczynowo-skutkowym działa w takim samym czasie klasycznym („dodatnim”), jak film normalny. Może to ułatwiać wyobrażanie sobie, ale nic poza tym.

W fizyce kwantowej odpowiednim symbolem graficznym, sugerującym, że pojęcie czasu w fizyce kwantowej jest diametralnie odmienne, mógłby być np. pseudowektor pozbawiony długości, czyli modułu, zachowujący jedynie zwrot i punkt przyłożenia. Wszystko to wydaje się jeszcze do przyjęcia, rzecz jednak w tym, że tych zwrotów może być w „nadprzestrzeni” nieobliczalnie (a nawet być może nieskończenie) wiele, natomiast we Wszechświecie mogą być tylko cztery i muszą być ortogonalne. W tym miejscu dla wyobraźni czai się pułapka: nie można utożsamiać omawianych zwrotów z kierunkami w przestrzeni (geograficznymi), np. kierunkami ruchu. Ponadto te symbole nie oznaczają cząstek materii w ruchu, są tylko graficznym zapisem tego, do jakiej kategorii materii (lub w ogólnym znaczeniu energii) cząstka albo ich układ fizyczny zostają naznaczone wtedy, gdy się stają tą cząstką bądź zespołem cząstek.

Kosmologiczna zasada przyczynowości nie jest moim pomysłem. Ważną dla mnie inspiracją były natomiast prace trójki wybitnych teoretyków, profesorów: Jerzego Jurkiewicza z UJ, Jana Ambjorna z Niels Bohr Instytute w Kopenhadze oraz Renate Loll z Utrecht University. W szczególności mam na myśli publikację „Świata Nauki” nr 8, 2008, pt. Samoorganizujący się kwantowy wszechświat (polskie wydanie Scientific American.) Autorzy stosują graficzne oznaczenie kierunków przyczynowości i skutkowania za pomocą strzałek. Ja pójdę podobną drogą. (Ilustracja 3-1).

Można sobie to wyobrazić jako naznaczenie cząstki lub grudki materii stygmatem czasu kwantowego. Tych stygmatów nie można się już pozbyć. Stygmat nieodwracalnie zaszeregowuje cząstkę lub kwant energii do określonego łańcucha przyczynowo-skutkowego, który odtąd będziemy nazywać pragmą (arbitralny skrót greckiego słowa pragmatikotita, πραγματικότητα, rzeczywistość, wszystko, co istnieje. Liczę na to że bracia Grecy mi wybaczą taką śmiałą ingerencję w ich wspaniały język.) Celowo chcę uniknąć terminu „rzeczywistość” (ang. reality), powszechnie używanego w języku polskim, ponieważ tej powszechności nie towarzyszy jedna dostatecznie ścisła definicja bądź jedno powszechne rozumienie tego terminu.

Ilustracja 3-1. Ortogonalne stygmaty czasu kwantowego jako: monopole, duopole, kwadrupole i heksapole. Heksapol powstaje z kwadrupola przez dodanie pary stygmatów (w kolorze ciemnobrązowym), odnoszącej się do przepływów informacji (proszę zwrócić uwagę na kierunki strzałek w tej parze)

W celu ułatwienia wyobrażenia sobie czasu klasycznego, ale skierowanego w nieobliczalną ilość kierunków przyczynowości, posłużę się przykładem klocków domina, ustawionych na wąskich ściankach, szerokimi ściankami równolegle do siebie, wzdłuż linii prostej, tak jak pokazano na ilustracji 3-2. Każdy z dwóch rzędów klocków reprezentuje oddzielną „rzeczywistość”, której zmiany pokazują kolejne upadki klocków popchniętych przez najbliższy klocek „z przeszłości”. Ilustracje pokazują także sens ortogonalności, na którą będziemy w tej opowieści jeszcze często się powoływać.

Na ilustracji 3-3 pokazana jest nieuchronna kolizja wskutek tego, że dwa klocki znalazły się w tym samym miejscu. Następuje katastrofa unicestwiająca obie rzeczywistości, co pokazuje sferyczna ognista łuna.

Przyjrzyjmy się uważnie tej ilustracji. Przecież można uniknąć katastrofy, jeżeli jeden z ciągów zostanie przesunięty wzdłuż osi czasu o zaledwie połowę odstępu klocków. Wtedy oba rzędy klocków będą się przewracać nadal, jakby nie „odczuwając” obopólnej obecności. I tu w najprostszy możliwy sposób pokazane są działanie i sens jednego z najważniejszych praw fizyki…kwantowej, tzw. zakazu Pauliego. Zakaz ten uniemożliwia dwóm cząstkom o takim samym stanie kwantowym znalezienie się w tym samym miejscu. Złamanie tego zakazu oznaczałoby, że obie cząstki, a prawdopodobnie także sąsiednie, podzieliłyby los tych pokazanych na ilustracji 3-3.

Rzadko się zdarza, że skomplikowane matematycznie prawo fizyki kwantowej można pokazać na obiektach makroskopowych, dlatego pokazana na ilustracjach 3-2, 3-3 i 3-4 zabawa z klockami domina jest zaskakującym, ale zapewne przypadkowym zbiegiem analogii.

Ilustracja 3-2. Dwa ortogonalne ciągi klocków domina jako dwie odrębnie realizujące się „rzeczywistości kwantowe” (pragmy)

Roger Penrose, niekwestionowany autorytet współczesnej matematyki i fizyki, w swoim wielkim (1100 stron), wiekopomnym i pięknie wydanym dziele pt. Droga do rzeczywistości (Prószyński, 2010. Wspaniały przekład Prof. Jerzego Przystawy, 1939 – 2012), usiłuje zdefiniować tytułowy byt w pierwszym i ostatnim rozdziale księgi. To bardzo interesujący zabieg: porównanie poglądu Autora na wstępie dzieła i po jego zakończeniu. Nie okazało się to dla wielkiego uczonego zadaniem łatwym, skoro na początku do zakresu znaczeniowego Reality zaliczył świat fizyczny, świat idei matematycznych i świat mentalny, przy czym relacje miedzy tymi „światami” wcale nie są dla Niego oczywiste. No, może z jednym wyjątkiem: świat „platoński”, czyli świat idei matematycznych, któremu nadaje zamiennie nazwę Świata Prawdy, bezdyskusyjnie zarządza całym światem fizycznym. Sir Roger zamyka swoją Księgę uzupełnieniem pierwotnej wizji przez rozróżnienie w świecie idei trzech pochodnych: Prawdy (czyli praw matematycznych) i Piękna przeplatającego się ze światem fizycznym. Trzecią jest… Moralność, obejmująca także w całości świat mentalny. Oto, którędy wiedzie droga do rzeczywistości, pisze Autor, niejako wyjaśniając tytuł swojego dzieła, znacznie wykraczającego poza sferę czystej fizyki i matematyki.

Ilustracja 3-3. Kolizja dwóch ciągów, których ortogonalnie położone klocki domina znalazły się w jednym miejscu, w takim samym „stanie kwantowym”. Dwa kwanty (czyli klocki domina) o takim samym stanie kwantowym nie mogą się znaleźć w jednym miejscu (w tym samym kwancie przestrzeni). Prawa fizyki kwantowej tego zabraniają, dowodem słuszności tego prawa jest istnienie nasze i Wszechświata

Ilustracja 3-4. Dwa ortogonalne ciągi domina bez kolizji, dzięki przesunięciu jednej grupy klocków względem drugiej o co najmniej połowę jednego odstępu. Można to uważać za poglądowy przykład zachowania zakazu Pauliego w fizyce kwantowej, co chroni układy kwantowe przed katastrofą termiczną i warunkuje ich istnienie. Jest to także ułatwiający wyobraźnię układ quasikwantowy (klocki to kwanty materii lub po prostu energii), pokazujący, że jest możliwe współistnienie dwóch odrębnych rzeczywistości (pragm w jednym rejonie nadprzestrzeni), jeżeli tylko są one ortogonalne w rozumieniu kosmologicznej zasady przyczynowości

Zazwyczaj przez rozpowszechniony termin rzeczywistość rozumie się to, co indywidualnie lub zbiorowo postrzegamy w świecie analogowym, ale nie kwantowym. Kosmologiczne pojęcie rzeczywistości nosi w sobie pułapkę, bo prowadzi do postawy mentalnej typu: „ja i kosmos”. Właśnie dlatego zdecydowałem się na wprowadzenie odrębnego, może trochę dziwnego terminu pragmata, przez który chcę zasugerować z gruntu odmienną postawę mentalną, a mianowicie: „ ja, jako organiczna część kosmosu”.

Z tego, co napisałem, wynika, a przynajmniej powinno wynikać, że oprócz wieloznacznej rzeczywistości klasycznej istnieje także „rzeczywistość kwantowa”. Uznaję więc za logiczne, a nawet niezbędne, rozróżnienie znaczeń tych terminów przez odrębne nazwy. Czy można wyobrazić sobie naszą obecność w rzeczywistości kwantowej? Tak, jeśli ta wyobraźnia jest dostatecznie bujna, a jej nosiciel nie ma zbyt wiele skrupułów, choć przestrzegałem wcześniej, że z usiłowaniami rozszczepienia świadomości nie ma żartów. Wynik jednej z takich prób pokazałem na Ilustracjach 3-5 i 3-6.

Ilustracje te według zamiaru autora przedstawiają nadprzestrzeń (czarne tło ilustracji) z migocącymi efektami współdziałania obu pól: Χ i Ψ, o których wspominałem wcześniej. „Produkcja” cząstek materii w postaci najpierw monopoli, a potem duopoli, odbywa się nieprzerwanie, a pierwszymi inicjatorami tej kreacji są fluktuacje informacji w każdej komórce pola Ψ. Wyobraźmy sobie, że informacja musi wytwarzać fluktuacje „informacji o samej sobie”, a w odpowiedzi pole Χ wytwarza „fluktuacje materii”, czyli coś w postaci zmaterializowanego szumu. Ten szum pozostaje bytem chaotycznym dopóty, dopóki nie pojawią się wraz z nim cząstki naznaczone pojedynczym stygmatem czasu, jako monopole nadal rozrzucone w nadprzestrzeni początkowo chaotycznie, a następnie w wyniku „poszukiwania ortogonalnego partnera”, zamieniające się w duopole, które z kolei łączą się w pary ortogonalnych duopoli, czyli w kwadrupole. Co może być powodem takich poszukiwań i łączenia się? Sądzę, że tą sprawczą energią może być jedynie grawitacja. Jeśli to przypuszczenie jest słuszne, oznaczałoby to, że protocząstki, jakimi są monopole i duopole, obdarzone są, oprócz stygmatów czasu, także ładunkami grawitacji, czyli grawionami, być może w ułamkowej ich części, podobnie jak to się dzieje z ładunkami elektrycznymi.

Powyższy opis kreacji materii jest czysto spekulatywny, nie jest oparty na jakichkolwiek przesłankach naukowych i dlatego musi być potraktowany, jako „opowieść o Kosmosie”, zresztą tak jak cała ta książka. Spodziewam się natomiast, że radykalni racjonaliści i materialiści oburzą się na sugerowaną tutaj pierwotność Słowa.

Czerwone kropki na pokazanych ilustracjach to jeden ze składników Wszechświata: informacja lub raczej kwanty informacji, a w tym konkretnym wypadku wszystko to, co w świecie analogowym staje się nieuchwytne, zarówno to, co uświadomione, jak i to, co nieuświadomione. Jasnoniebieskie kropki natomiast oznaczają cząstki materii już zorientowane kierunkami stygmatów czasu.

W skrócie przedstawiony wyżej domniemany proces kreacji materii nazwę metafizyką egzystencji każdego bytu fizycznego emanującego jakąkolwiek informację. Jak się dalej okaże, informacja, abstrakcyjne pojęcie w fizyce klasycznej, nabiera także wymiernego znaczenia energetycznego w zaprezentowanej tu hipotezie kwantowej. To stanowi sens pojęcia pragma, zamiast utartego terminu rzeczywistość.

Informacja jest fundamentalnym czynnikiem warunkującym istnienie Wszechświata i wszelkich materialnych bytów z człowiekiem włącznie. Bez informacji nie byłoby tzw. oddziaływań fizycznych na odległość, zmuszających poważnych kosmologów do traktowania Wszechświata jako integralnej całości. To niezmiernie trudne, o wiele łatwiej jest badać jakiś fragment Wszechświata, a następnie rozciągać uzyskane wyniki jako wiarygodne dla jego całości. Jednak często badacze są zmuszeni do takiego „lokalnego” postępowania w myśl nadziei, że nawet takie wyniki zawierają jakąś wskazówkę dla dalszego toku badań.

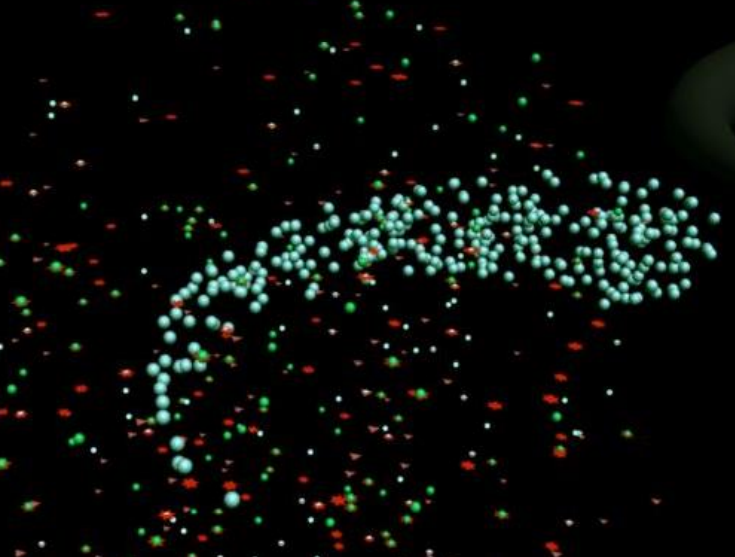
Ilustracja 3-5. Generowanie nowego Wszechświata lub multiwszechświata w nadprzestrzeni, czyli porządkowanie chaotycznego początkowo rozkładu monopoli przez łączenie się ich w ortogonalne duopole, a następnie w kwadrupole. Tak, być może, powstają sprzężone grawitacyjne materialne cząstki Wszechświata

Ilustracja 3-6. Generowanie nowej protogwiazdy, która może okazać się macierzystą dla multiwszechświata cyklicznego. (Nasz Wszechświat jest składnikiem takiego multiwszechświata, tworząc zaledwie jeden z jego cykli)

1.4 Przestrzeń i nadprzestrzeń. Kwanty przestrzeni, czyli spacjony.

W jednym z możliwych wszechświatów, w tym, który właśnie rozpatrujemy, stygmaty niby czasu, o których pisałem wyżej, mogą być tylko (i aż) cztery i muszą być wzajemnie ortogonalne.

Termin „ortogonalność” w geometrii jest matematycznie dość zrozumiały. Istotą ortogonalności wielkości wektorowych w języku matematyki jest zerowanie się tzw. iloczynu skalarnego. W najprostszym i najłatwiejszym wyobrażeniu ortogonalność jest równoznaczna z prostopadłością wektorów w przestrzeni trójwymiarowej. W mojej hipotezie kosmologicznej ortogonalizacja oznacza także „wbudowany” we Wszechświat mechanizm samoorganizacji i samonaprawiania. Wrócę do tego dalej.

Warto w tym miejscu wspomnieć o ciekawostce dotyczącej kosmologicznych aspektów liczby 4 w ziemskim systemie liczbowym. Ta cyfra, jako iloraz lub wartość niektórych wielkości kosmologicznych, występuje w kilku znanych mi przypadkach, pozornie niezwiązanych bezpośrednio ze sobą. Pierwsze zdanie rozdziału jest właśnie jednym z takich przypadków. O innych napiszę w odpowiednim do tego miejscu, ale już teraz nie mogę nie przywołać twórczości p. Olgi Tokarczuk i rozdziału pt. „Czas rzeczy poczwórnych” w powieści Prawiek i inne czasy. (Artystyczne związki twórczości p. Tokarczuk z pięknem i harmonią, a niekiedy okrucieństwem Kosmosu, są dla mnie czymś zdumiewającym).

Wspomniane wyżej stygmaty czasu tworzą monopole, duopole i kwadrupole. Rozwinięcie tego pomysłu znajdzie się w rozdziale „Składniki Wszechświata”.

A gdzie w takim razie są pozostałe stygmaty?

Odpowiedź na postawione wyżej pytanie brzmi: w niewyobrażalnej mnogości innych wszechświatów zanurzonych w nadprzestrzeni, która jest macierzą i kolebką wszystkich wszechświatów i wypełnia całą możliwą do wyobrażenia przestrzeń pozbawioną granic. W literaturze naukowej i popularnonaukowej stosowany bywa termin „hiperprzestrzeń”, ale pragnę go uniknąć. Podoba mi się także termin grecki „topos” (τόπος), który w znaczeniu geometrycznym bywa przetłumaczony jako „miejsce wspólne dla wszystkich miejsc”. Jest to więc pojęcie nie tylko matematyczne, lecz również filozoficzne.

Umówmy się, że kiedy mam na myśli „nasz” Wszechświat, tzn. ten, który obserwujemy i którego jesteśmy cząstką, piszę o nim, poczynając od wielkiej litery, czyli Wszechświat.

Bez dużej litery na początku termin będzie oznaczać dowolny z mnogości możliwych wszechświatów. A jeżeli okaże się, że grupy tych wszechświatów mogą tworzyć powiązane ze sobą fizycznie gromady (podobnie jak to ma miejsce z galaktykami i gwiazdami), to takie „gromady” będę nazywać wielowszechświatami (proszę wszakże nie utożsamiać z „multiświatami” Everetta i Gribbina).

Moja hipoteza zaczyna się i kończy na bezgranicznej nadprzestrzeni i nie mam najmniejszego zamiaru lub ambicji, a zwłaszcza kompetencji, by te granice przekroczyć w kierunku na „wcześniej”. Próby odpowiedzi na pytanie: skąd się wzięła nadprzestrzeń i co jest poza nią?, pozostawiam innym śmiałkom.

Przestrzeń fizyczna staje się nią wtedy, gdy zostaje wypełniona jakąkolwiek energią, materią, promieniowaniem, polem, oczywiście w notacji probabilistycznej.

Energia wypełniająca jakąś przestrzeń ma postać kwantową, a zatem i przestrzeń musi mieć postać ziarnistą. Obserwator kwantowy widziałby ją jako chmurkę prawdopodobieństwa o zróżnicowanej gęstości. Sądzę, że u wielu osób zrodzi się pytanie, jaki jest kształt „atomów” przestrzeni? Użycie analogii do atomu nie wydaje się w pełni trafne, jako że atom jest bytem złożonym. Powstaje w związku z tym potrzeba nazwania elementarnej „cząstki przestrzeni probabilistycznej”. Jest to już posunięcie na tyle śmiałe i ryzykowne, że można mieć pewność stanowczej krytyki ze strony zarówno fizyków, jak i językoznawców.

Niestety, nie mam innego wyjścia i na określenie elementarnego ziarna przestrzeni kwantowej proponuję nazwę spacjon (z łacińskiego spatium, czyli przestrzeń). Wiązka spacjonów może mieć charakter falowy, tak jak materia, i takie fale nazwę falami spacjonowymi. Mogą być fale „grawitacyjne”, mogą więc także być fale spacjonowe, na razie jako hipotetyczne.

Jeśli chodzi natomiast o kształt spacjonów, to tak samo można dociekać (raczej bezowocnie) kształtu cząstek elementarnych, elektronów i kwarków.

Każdy kształt powinien dać się matematycznie opisać i jest to możliwe, ale nie w nadprzestrzeni, gdzie nie ma żadnego punktu odniesienia jako środka układu współrzędnych. Rozumowanie, że przejściu od przestrzeni kwantowej do analogowej, czyli zwiększaniu prawdopodobieństwa do wartości bliskiej 1, powinno towarzyszyć coraz dokładniejsze wypełnienie nadprzestrzeni, aż odległości między spacjonami przyjmą wartość zerową, sugerowałoby kształt tych ostatnich jako figur platońskich, sześcianu albo ośmiościanu. Te figury mogą całkowicie wypełnić przestrzeń analogową. Nie jest to możliwe nie tylko z powodu nieistnienia zera i jedności, ale przede wszystkim byłoby to równoznaczne ze złamaniem podstawowej zasady fizyki kwantowej, jaką jest tzw. zakaz Pauliego. Sąsiadujące spacjony mogłyby mieć identyczne stany kwantowe, co skutkowałoby anihilacją ich zawartości i zawaleniem się budowanej w wyobraźni konstrukcji.

Fizycy klasyczni wolą niekiedy raczej uznać, że jeśli nie ma we fragmencie przestrzeni żadnej materii, promieniowania, pola i w ogóle żadnej ze znanych postaci energii, to znaczy, że nie ma tam niczego, jest „próżnia”. Wobec coraz większych kłopotów z pojęciem próżni pojawiły się takie terminy, jak „fluktuacje kwantowe” i „ ujemna energia próżni”.

W tej opowieści nie powinno być miejsca na tak subtelne rozważania teoretyczne lub wyobrażenia, niekiedy jednak muszę się do nich odwołać, bo nie jestem w stanie zaproponować czegoś innego, co byłoby w miarę przekonujące. Wszelkie „nadwyżki przestrzeni” są wypełnione tymi samym bytami fizycznymi, co nadprzestrzeń, a mianowicie dwoma polami, z których jedno oznaczam grecką literą Χ (chi), a drugie grecką literą Ψ (psi).

Pierwsze jest polem energetycznym, tzn. dostarcza ono kwantu energii (masy) w odpowiedzi na kwant informacji pola informacyjnego Ψ. Oba pola mają wspólną cechę fizyczną: ich szybkość propagacji jest nieskończenie wielka, a więc są wszechobecne. Pomysł tych pól wchodzi raczej w zakres kosmogonii, przynajmniej w mojej hipotezie, i do niej jeszcze powrócę. We współczesnej nauce jest natomiast realną podstawą tzw. fizyki Higgsa, wyjaśniającej fenomen powstawania mas z udziałem pola energetycznego Hi i bozonu Higgsa, zwanego niekiedy „boską cząstką”. Osobiście mam wątpliwości, czy do współdziałania obu pól jest niezbędny jakiś, nawet najbardziej boski, bozon.

1.5 Geometrie przestrzeni.

Zazwyczaj rozróżnia się geometrię euklidesową i geometrię nieeuklidesową. Podział ten jest tak rozpowszechniony, że nie wymaga dodatkowych objaśnień. Niezwykle ważną sprawą będzie natomiast rozróżnienie geometrii eliptycznej (w tym sferycznej) i geometrii hiperbolicznej, z którą nie mamy zwykle do czynienia, przynajmniej w sposób świadomy.

Geometria sferyczna zasadza się na funkcjach trygonometrycznych, które poznajemy już w szkołach średnich. Odpowiednie funkcje hiperboliczne są na ogół nieznane, bo nie mamy takiej potrzeby, a ponadto wymagają w obliczeniach specjalnego, nie zawsze dostępnego, oprogramowania. W przypadku kosmologii taka potrzeba istnieje, a nawet staje się koniecznością.

O zakrzywieniu przestrzeni, a właściwie czterowymiarowej czasoprzestrzeni, dowiadujemy się zazwyczaj wtedy, kiedy przywołuje się ogólną teorię względności (OTW). Trwa to już ponad 100 lat. Dowiadujemy się, że to zakrzywienie ma miejsce w pobliżu wielkich mas i powoduje efekt grawitacji ujawniający się jako ich wzajemne przyciąganie się zgodnie z prawem powszechnego ciążenia Newtona. Niestety, w czasach Einsteina królował pogląd, że Wszechświat jest bezwzględnie stabilny i OTW z wielką ścisłością ten pogląd potwierdzała, choć do wyjaśnienia obserwowanego rozszerzającego się Wszechświata potrzebne były „drobne poprawki” w postaci tzw. stałej kosmologicznej. Obecnie, wobec napływu danych obserwacyjnych, już nie jest to wystarczające. Pojawienie się w nauce takich terminów, jak „ciemna materia” i „ciemna energia”, jest oznaką czasowej bezradności badaczy. „Ciemna” to znaczy taka, o której nie możemy jeszcze nic pewnego powiedzieć.

Krzywizna to nie tylko atrybut krzywej lub przestrzeni dwu- albo trzy- i czterowymiarowej, to także konkretny, teoretycznie obliczalny parametr w zapisie matematycznym, który jest wartością dodatnią (w geometrii eliptycznej) lub wartością ujemną (w geometrii hiperbolicznej). Krzywizna zerowa oznacza, że jesteśmy w zakresie geometrii euklidesowej i rozważamy figury płaskie, których nie znajdziemy w kosmologii kwantowej i raczej wyjątkowo w kosmologii klasycznej, chyba że mamy do czynienia z figurami wielkoskalowymi o jednakowych średnich bezwzględnych wartościach krzywizn dodatniej i ujemnej i jeśli wystarcza nam znajomość średniej krzywizny w rozpatrywanej skali. Powszechne jest w literaturze popularnonaukowej odróżnianie znaku krzywizny powierzchni przez sumę kątów w trójkącie naniesionym na te powierzchnie w sposób projekcyjny, czyli bezwzględnie przylegający. Suma tych kątów wynosi 180 stopni tylko na powierzchniach płaskich. Na powierzchniach o krzywiźnie dodatniej jest ona większa, a na powierzchniach o krzywiźnie ujemnej mniejsza od 180 stopni.

Powierzchnie brył o krzywiźnie ujemnej sprawiają duży kłopot w grafice. W literaturze operuje się na ogół rysunkami powierzchni 2D w kształcie siodła hippicznego. Takie ilustracje niczego w kosmologii nie rozwiązują, ponieważ często (zwłaszcza przy rozważaniu ewolucji w czasie klasycznym) musimy operować powierzchniami 3D, zamkniętymi, a nie otwartymi, których krzywizny muszą być dokładnie znane i obliczalne. Niestety wymykają się one naszej wyobraźni, a w następstwie skutkuje to koniecznością sięgania po specjalne podprogramy graficzne, jeżeli w ogóle takie są dostępne.

Dla zilustrowania problemu na rys 5-1 przedstawię powierzchnię wyjątkową, chyba niedocenioną w kosmologii, a mianowicie powierzchnię torusa. Górna i dolna część powierzchni zewnętrznej torusa mają krzywiznę (zdefiniowaną matematycznie jako tzw. krzywiznę Gaussa) dodatnią (i zerową na największym równoleżniku), natomiast lewa i prawa części powierzchni wewnętrznej mają krzywiznę ujemną. Można to lepiej zobaczyć na figurze 3D, będącej komplementarnym uzupełnieniem torusa do postaci dysku. Zaproponowałem dla tej figury (górna prawa część rysunku) nazwę pseudotorus. Chodzi m.in. o to, aby nie mylić tej figury z figurami obrotowymi wyznaczonymi przez łuk o rozwartości π (pi) radianów wokół osi dowolnie odległych od łuku. Oczywiście pseudotorus nie spełnia wszystkich warunków ujemności krzywizny, ponieważ kołowe powierzchnie, górna i dolna, zamykające całą figurę, mają krzywiznę zerową. Musiałyby być powierzchniami hiperbolicznymi, co graficznie bardzo problem komplikuje. Niemniej jednak pseudotorus i utworzony z jego udziałem dysk okażą się bardzo przydatnymi tam, gdzie ich wysokość nie ma krytycznego znaczenia i można założyć, że zmierza do nieskończoności. Rysunek pseudotorusa w konwencji siatkowej pokazuje ważną rzecz, a mianowicie linie geodezyjne (zwane w skrócie po prostu geodezyjnymi) mające oczywiście krzywiznę ujemną. Jest to istotne przy konstruowaniu innych figur na podstawie znajomości geodezyjnych.

Ilustracja 5-1. Konstruowanie dysku z torusa o powierzchniach mających krzywiznę dodatnią oraz z pseudotorusa mającego boczne powierzchnie o krzywiźnie ujemnej.

A teraz najważniejsze: w jakim celu przedstawiam tu tak obszernie problem krzywizny, skoro czekają na nas jeszcze liczne inne kwestie, których wyobrażenie albo grafika nastręczają poważne kłopoty?

Odpowiedź może być zaskakująca, jeśli przywoła się wzmiankę o OTW, zrobioną na jednej z poprzednich stron. Wydaje się logiczne przekonanie, że skoro dodatnie zakrzywienie przestrzeni wokół mas powoduje (z wzajemnością) według OTW grawitację przyciągającą (nazwę ją dodatnią), to przestrzenie o krzywiźnie ujemnej dopuszczają bezkonfliktowo, tzn. bez anihilacji, do swego wnętrza jedynie te masy, które charakteryzują się grawitacją odpychającą, czyli ujemną. Przestrzeń dodatnia powoduje koncentrację materii, przestrzeń ujemna jej rozpraszanie. Waham się przed używaniem terminu „antygrawitacja”, dostatecznie skompromitowanego przez filmy s.f. Mógłbym właśnie w tym miejscu utracić jakąś grupkę czytelników, którzy z godnym mojego podziwu uporem dobrnęli aż do tego fragmentu. Problematyka grawitacji wymaga jednak oddzielnego szerszego opisania.

1.6 Grawitacja dodatnia i ujemna. Ładunki grawitacji.

1.6.1 Grawitacja nie tylko dodatnia czyli przyciągająca.

Nauka prawdopodobnie nie może uniknąć paradoksów i twierdzeń wewnętrznie sprzecznych. Współczesna nauka zawiera takich sporo: dualizm falowo-korpuskularny światła, paradoks bliźniąt i wiele innych. Nie jest to jakaś klęska nauki, wręcz przeciwnie, świadczą one, że badania eksperymentalne i teoretyczne sięgają do coraz bardziej szczegółowych i subtelnych zagadnień, a lista paradoksów jest jedynie katalogiem „spraw do załatwienia”, kiedy tylko nadarzą się ku temu odpowiednie warunki.

W poprzednim rozdziale wspomniałem o dwuznaczności skutków zakrzywienia przestrzeni przez masy grawitacyjne, ponieważ to samo zakrzywienie jest przyczyną zjawiska grawitacji. Nauka nie będąc w stanie uniknąć takich dwuznaczności, a właściwie rezygnując czasowo z zasady przyczynowości, toleruje je, jeśli tylko pozostają w polu jedynie interpretacji i nie doprowadzają do sprzecznych wyników obliczeń lub wniosków z obserwacji. Zasada przyczynowości jest jednak naczelną w mojej hipotezie, o czym uprzedzałem, można sobie na to pozwolić, skoro ma to miejsce poza nauką akademicką.

A zatem nasuwa się pytanie: co właściwie jest źródłem obu rodzajów grawitacji i jakim zasadom one podlegają?

1.6.2 Ładunki grawitacji czyli grawiony.

Poszukam analogii w elektromagnetyzmie. Przyjrzyjmy się danym CODATA (rozdz. 2.1), dotyczącym najlżejszej cząstki elementarnej, czyli elektronu. Pośród wielu danych w dziale atomistyki i fizyki jądrowej nie znajdziemy tam odnoszących się do ładunku elektrycznego, bez którego elektron lub antyelektron nie byłyby sobą. Znajdziemy je natomiast pod hasłem „elementary chargé” w dziale elektromagnetyzmu. Ładunek elektryczny elektronu został więc potraktowany jako coś osobnego lub wyjątkowego. Byłoby to zrozumiałe, gdyby w Modelu Standardowym znajdowała się poza elektronem i antyelektronem jakaś inna cząstka o dokładnie takiej samej masie i spinie, ale bez ładunku elektrycznego, podobnie jak to jest z protonem i neutronem. Ale takiej cząstki w Modelu nie ma. Jednostkowy, elementarny ładunek elektryczny publikacji CODATA wydaje się być osobnym bytem, stanowiącym o właściwościach elektronu i antyelektronu. W innych cząstkach, np. w kwarkach, jest również obecny, ale w wielkości ułamkowej. Ładunek musi mieć swój nośnik, istnienia wyizolowanego ładunku jeszcze nikt doświadczalnie nie stwierdził. Nauka przyjmuje za bardzo możliwe istnienie także ładunku magnetycznego (w moim domyśle o biegunowości N lub S), dla którego nośnikiem jest tzw. monopol magnetyczny, cząstka, która zdaniem kosmologów została wyemitowana w Wielkim Wybuchu w ilości takiej samej jak cząstki obdarzone ładunkami elektrycznymi. I tu sytuacja się powtarza, monopole powinny być, ale ich nie znaleziono.

Wróćmy do grawitacji. W niniejszej hipotezie sugeruję istnienie ładunku grawitacyjnego, którym w różnym stopniu (liczbie) są obdarzone wszystkie cząstki materii wykazujące dzięki temu własności grawitacyjne, dodatnie lub ujemne, zależnie od znaku ładunku. Nowo tworzony byt musi być jakoś nazwany. Proponuję nazwę grawion. W żadnym wypadku nie należy go mylić z grawitonem, który jest uznany przez naukę za cząstkę przenoszącą oddziaływania grawitacyjne, niebędącą budulcem Wszechświata (fermionem), lecz bozonem. W przeciwieństwie do naukowych grawitonów „moje grawiony” nie oddziaływują ze sobą, tak samo jak fotony. To bardzo komplikuje wykrywanie grawitonów i być może jest przyczyną tego, że nie zostały dotychczas potwierdzone doświadczalnie.

Czy to ma oznaczać, że OTW jest błędna? Stanowczo zaprzeczam podobnym przypuszczeniom, przestrzeń „robi swoje” i zakrzywia się w obecności mas zawierających grawiony, natomiast liczba grawionów w tych masach może być zmienna w zależności od wartości i znaku krzywizny. Masy grawitacyjne także „robią swoje” i wpływają na wielkość i znak krzywizny przestrzeni. Każda strona wie, co ma robić zgodnie z OTW, ale przynajmniej jest wiadome, co jest tych zjawisk przyczyną, mianowicie ładunki grawitacyjne, czyli grawiony, lub, w szerszym znaczeniu, pole grawionowe. Hipotetyczne grawiony nie mają swojej odrębnej masy, tak jak i ładunki elektryczne, natomiast nośniki ładunków masę mają. Jak się jednak okaże dalej, grawiony mogą wpływać na chwilową wartość masy cząstek poruszających się z szybkością porównywalną z szybkością światła i wtedy, gdy mają przyśpieszenie, czyli gdy ich szybkość się zwiększa albo zmniejsza. Szansa na związanie grawitacji z klasycznym czasem jest atrakcyjna. Traktowanie grawitacji jako niezmiennej właściwości mas, niezależnie od tego, czy one są w spoczynku, czy poruszają się względem innych mas, bez dowodów teoretycznych lub doświadczalnych, wydaje się pochopne. Podobne wątpliwości nasuwają się w kwestii izotropowości pola grawitacyjnego. Czy natężenie pola grawitacyjnego naprawdę nie zależy od kształtu zwartego skupiska materii (np. atomu, planety, gwiazdy, gromady i in.) i kierunku jego emisji?

Ta ostatnia wątpliwość pojawiła się we mnie po zapoznaniu się z książką pt. Grawitacja, bezwładność, masa, przestrzeń, (279 stron), opublikowaną tylko w Internecie, autorstwa p. Ryszarda Wałka, wydanie 5, 2017. Przypuszczam, że ta obszerna i bardzo starannie przygotowana publikacja nie znalazła wydawcy, ponieważ wiele wyrażonych w niej twierdzeń Autora nie pokrywa się z nauką akademicką. Przypomina to trochę przedstawianą tu hipotezę. Należy ubolewać, że ta książka, przeznaczona dla czytelników raczej dobrze wprowadzonych w tematykę, nie doczekała się w ciągu kilku lat jej obecności w Internecie śladu zainteresowania lub jakiejkolwiek recenzji ze strony ludzi nauki. Czyżby zniżanie się do lektury tego rodzaju pozycji było aż tak godzące w prestiż naukowca?

1.6.3 Prawa grawitacji.

Właściwie znamy tylko jedno prawo grawitacji, jest to prawo powszechnego ciążenia sformułowane przez Newtona w 1687 roku, określające wielkość siły tego ciążenia wyrażoną wzorem znanym od „czasów szkolnych”:

Znaczenie użytych symboli jest tak powszechnie znane, że nie wymaga tu wyjaśnień. Przypomnę jedynie, że stała grawitacji G jest wielkością fizyczną, charakteryzującą średnią grawitację dodatnią (przyciągającą) w dowolnej, wybranej arbitralnie, kostce lub kulce przestrzeni, wyrażoną w jednostkach,

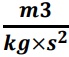
jeśli siła F ma być wyrażona w newtonach (N).

Siła jest wielkością wektorową, po prawej stronie Newtonowskiego równania powyżej znajduje się natomiast wielkość skalarna, co rozumie się zwyczajowo tak, że zwrot siły F jest zawsze w kierunku ciała M, ponieważ grawitacyjny wpływ ciała m uznaje się za pomijalny. Nauka z tego impasu wychodzi formalnym, mało eleganckim trickiem z użyciem w liczniku tzw. wersora, wektora ze zwrotem zgodnym ze zwrotem siły F oraz sześciennego wykładnika potęgowego w mianowniku. Wszystko po to, żeby matematycznemu formalizmowi stało się zadość. Jestem przekonany, że Wszechświat nie jest aż tak przebiegły, jestem raczej skłonny podejrzewać, że ma tu miejsce jakieś nieporozumienie merytoryczne.

Moja notacja równania będzie więc następująca:

Zastosowany tu zapis wektorowy

wynika stąd, że podaję w wątpliwość izotropowość pola grawionowego w obecności pola (lub fali) spacjonowej, dynamicznie zniekształcającej ciało grawitacyjne i zmieniające rozkład ładunków grawitacyjnych w tym ciele. W takim przypadku wartość G mogłaby być liczbą zespoloną i byłaby różna w różnych kierunkach przestrzeni analogowej. Na razie proszę o przyjęcie tego „na wiarę”, wrócę do sprawy w następnych rozdziałach, być może w sposób przekonujący.

Jeżeli mamy zamiar zagłębiać się w dalszą część niniejszej hipotezy, musi tu zostać sformułowana nowa zasada odnosząca się do grawitacji ujemnej, czyli odpychającej. Według mojego rozeznania takiej zasady nikt jeszcze nie ujawnił w notacji analogicznej do Newtonowskiej (chociaż stwierdzono, że oddziaływania kwarków ze sobą są odpychające i rosną z kwadratem ich odległości), więc zrobię to ja, wyłącznie na potrzeby tej hipotezy. Od razu zaznaczam, że jeśli okaże się ona słuszna, tzn. potwierdzona kiedyś doświadczalnie, będzie to owoc jedynie naturalnego myślenia logicznego.

Większość wielkości fizycznych we Wszechświecie, jak się okazuje w miarę zagłębiania się w kosmologię, ma charakter dualny, czyli ma swoje odpowiedniki komplementarne, często z przedrostkiem anty-, tworzące w sumie jakąś imaginowaną całość. Tak jest przecież z materią i antymaterią, a najdobitniej widać to w teorii supersymetrii cząstek, która jednak nie doczekała się jeszcze miejsca w Modelu Standardowym.

Jest zatem logiczne i chyba nie wymaga „objawienia”, że skoro siła przyciągająca grawitacji dodatniej maleje z kwadratem odległości od jej źródła, to siła odpychająca grawitacji ujemnej „powinna” rosnąć z tym kwadratem, podobnie jak to się dzieje z kwarkami. Słowo powinna będę dalej rozumiał jako faktycznie istniejącą właściwość fizyczną jednego z rodzajów grawionów. Uzurpatorskie prawo grawitacji ujemnej będzie więc wyrażało się wzorem:

gdzie

oznacza wektorową wartość stałej grawitacji ujemnej wyrażoną w (kg x m x s²)^-1, jeśli siła F ma być wyrażona w newtonach. Odwrócenie strzałek ma sugerować, że chodzi o odwrotny znak grawitacji.

Tu jednak pojawiają się poważne wątpliwości: co właściwie znaczą fizycznie obie „stałe grawitacyjne”? Jakiego bytu fizycznego są właściwością: przestrzeni, materii? Czy stała G podana przez CODATA charakteryzuje grawitację całego obserwowalnego Wszechświata, czy jedynie maleńki sześcian lub maleńką sferę przestrzeni, zawierającą wewnątrz planetę Ziemia albo może całą Galaktykę?

Wyprzedzam dalsze rozważania o budowie i ewolucji Wszechświata i ośmielam się twierdzić, co następuje:

Po pierwsze: obie „ stałe” (tak będę je dalej nazywał, żeby nie powiększać chaosu terminologicznego) nie są stałe, w świecie klasycznym podlegają ewolucji w czasie razem z całym Wszechświatem. W żadnym razie podane przez CODATA wartości G nie charakteryzują całego Wszechświata, a jedynie, i to po uśrednieniu, znikomą jego część, w której się znajdujemy albo gdzie właśnie dokonywany był i nadal bywa pomiar tego parametru. Właśnie parametru, a nie jednej ze stałych fizycznych lub kosmologicznych. Oba parametry, G i g^* są wynikami takiego, a nie innego, rozmieszczenia materii i grawionów we Wszechświecie, i ich lokalne wartości charakteryzują nie przestrzeń ani nie materię, ale lokalny rozkład ładunków grawitacyjnych w całym Wszechświecie o bardzo niejednorodnym rozkładzie materii. Zaprzeczam więc licznym i ciągle jeszcze powtarzanym zapewnieniom nauki o jednorodności rozkładu materii Wszechświata. W sposób ewidentny zaprzeczają temu wyniki zaledwie 9-miesięcznej misji satelity Planck, podane do publicznej wiadomości na wspomnianej wcześniej konferencji prasowej 21.03.2013 r. Niejednorodność promieniowania tła oceniana przez ESA na 10^-5 nie powinna wydawać się mała w skali kosmicznej, zwłaszcza na południowej stronie sfery obserwowalnego Wszechświata.

Po drugie: klasyczny wzór Newtona na siłę grawitacji ma znikome bezpośrednie zastosowanie w matematyce Wszechświata. To, co jest możliwe do przyjęcia w warunkach laboratoryjnych na Ziemi lub na powierzchni innej planety, tzn. kiedy można pomijać oddziaływania grawitacyjne innych mas poza masą źródłową (M) i próbną (m), jest nie do przyjęcia w warunkach kosmologicznych, w których energie grawitacyjne stanowią ponad 50 % całkowitej energii wypełniającej Wszechświat. Dla matematyków byłoby zapewne ułatwieniem, gdyby o grawitacji Wszechświata decydowała jedna olbrzymia masa, np. jakiejś protogwiazdy, a pozostała część energii grawitacyjnej pochodziła od równomiernie rozproszonej masy gwiazd i planet, stanowiącej, według oceny naukowców, nie więcej niż 4,5% masy całego obserwowalnego Wszechświata. Nawet w ziemskich warunkach laboratoryjnych, jeżeli oprócz mas M i m₁ wprowadzi się trzecią masę m₂, sprawa bardzo się matematycznie komplikuje, zwłaszcza wtedy gdy masa m₁jest porównywalna z masą M i mamy do czynienia z dwoma dużymi masami i jedną quasi-punktową (patrz Wikipedia: Problem n-ciał). Mimo tych trudności „Problem 3-ciał” został na tyle opanowany, że można z dużą dokładnością wyznaczać trajektorie Ziemi, Księżyca i Słońca, a także, co było bardzo potrzebne i pilne, wyznaczenie w tym układzie punktów równowagi („punktów Lagrange’a”), z których dwa, oznaczane symbolami L₄, L₅ są stabilne, a pozostałe L_1,L₂, L₃ są niestabilne (zob. Ilustracja 6-1). Jeden z tych punktów (L₂), odległy o około 1,5 miliona kilometrów od powierzchni Ziemi, wykorzystano do umieszczenia na orbicie w jego pobliżu Kosmicznego Obserwatorium Herschela oraz satelity Planck.

Ilustracja 6-1. Rozmieszczenie punktów równowagi (Lagrange’a) w układzie Słońce – Ziemia według Wikimedia Commons (Source Lagrange_points.jpg created by NASA. 12 August, 2009)

Z braku dostatecznej wiedzy nie jestem w stanie rozwinąć tego niezwykle interesującego problemu i nie ma, jak sądzę, takiej potrzeby w prezentacji mojej hipotezy. Wyprzedzę nieco dalsze jej części (dość ryzykownym, przyznaję) stwierdzeniem:

Wszechświat wypełniony jest ładunkami grawitacyjnymi w sposób wysoce niejednorodny, anizotropowy, i uśrednione wartości stałych G oraz g^* charakteryzują jedynie dowolnie wybraną „kostkę” lub „kulkę” przestrzeni. Im ta próbna cząstka przestrzeni będzie mniejsza, tym dokładność wyznaczenia obu stałych będzie większa. Nie mamy z tym kłopotu, rozmiary Wszechświata są na tyle wielkie, że każdy lokalnie rozsądnie wybrany jego fragment może być uznany za dostatecznie mały, aby wartość stałej G, podana przez CODATA (6.674 08 x 10^-11 m³kg^-1s^-2z niepewnością standardową równą 0,00031×10^-11 m³kg^-1s^-2) uznać za dostatecznie dokładną przynajmniej w obrębie Układu Słonecznego. Te stałe mają atrybuty jak każda wielkość wektorowa: moduł, zwrot i punkt przyłożenia. W pewnym stadium ewolucji Wszechświat ewoluuje pod wpływem grawitacji tak, jakby rozkład rozproszonych w nim ładunków grawitacyjnych podyktowany był nie tylko przez jedno bardzo masywne centralne ciało (np. protogwiazdę w Wielkim Wybuchu), ale przez dwa takie ciała, różniące się między sobą stopniem tej masywności i gęstości i wcale nie wybuchające. Dalej zostanie to wyjaśnione w sposób uproszczony przez odwołanie się do opublikowanych (m.in. w Wikipedii) teoretycznych rozkładów pola grawitacyjnego dla układu Słońce – Ziemia – Księżyc, a także Jowisz –Słońce – trzecie ciało. Zakładam po prostu, że w dowolnym, odosobnionym układzie 3 ciał we Wszechświecie mapy pola grawitacyjnego będą bardzo podobne, a punkty szczególne L_1,L_2., L₃, L₄ będą na tych mapach również występować w takim samym usytuowaniu, jak względem Słońca, Ziemi i Księżyca.

w bardzo szerokim zakresie, od blisko zerowych w punktach L₄i L₅ dla G oraz w punktach L₁ i L₂ dla g^* do wielkich, zależnych od mas i rozmiarów każdego z dwóch ciał źródłowych. Ich zwroty zawierają się w kącie bryłowym 4π radianów. Z przytoczonych wyżej danych CODATA można by wnosić, że „nasze miejsce w Kosmosie” znajduje się blisko jednego z punktów L₄ lub L_5, ponieważ podana wartość G jest zastanawiająco mała. Istnieje jednak jeszcze inne hipotetyczne i całkiem nienaukowe wyjaśnienie przyczyn tak małej wartości G, ale także zakłada pewną wyjątkowość naszego miejsca w Kosmosie.

Zamierzony dalszy wywód wymaga pewnego, uprzedzającego, bardzo ważnego uzupełnienia tego rozdziału. Nasuwa się bowiem pytanie, jak zachowują się odosobnione pary swobodnych cząstek opisanych rodzajów materii, mających np. jednakowe masy ? W przypadku par cząstek elksjomaterii i sprochnomaterii wydaje się, że ich zachowania będą oczywiste: cząstki pierwszej pary będą dążyć do spotkania, drugiej będą się od siebie oddalać, w obu sytuacjach z szybkościami zgodnymi z prawami odwróconych kwadratów.

Najbardziej interesujące jest zachowanie pary cząstek, z których jedna należy do elksjomaterii, a druga do sprochnomaterii. Taka sytuacja wymaga bardziej szczegółowej naukowej analizy matematycznej, oczywiście przy założeniu, że arbitralnie zaproponowane „prawo grawitacji ujemnej” jest słuszne, albo jeżeli znane jest inne, bardziej wiarygodne. Z braku takiej analizy posłużę się, jak dotychczas, intuicją. Dla jednakowych mas: m₁= m₂= m oraz dla szczególnej wartości r₀możemy napisać następujące równanie na bazie fizyki klasycznej:

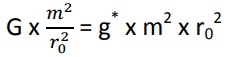
Rozwiązanie równania względem r₀daje wynik:

Gdy moduły „stałych” grawitacji dodatniej i ujemnej są istotnie stałe, to odległość obu cząstek jest wartością niezmienną bez względu na chwilowe położenie każdej z nich. Co więcej, z równania wynika, że wartość r_0,nie zależy od mas, a jedynie od relacji G i g^*.

Ten wniosek stanowi podstawę dalszego rozumowania nad siłami napędowymi ewolucji Wszechświata, co będzie przedmiotem rozdziału 9. Istotne dla procesów graficznego modelowania Wszechświata jest również to, że gdy moduły stałych grawitacyjnych G i g^* są równe, odstęp między oboma rodzajami cząstek jest równy 1 w przyjętej w modelowaniu skali. Ale uwaga: nie jest to graficznie tak proste, jakby się wydawało, ponieważ odstęp, o którym piszę, nie może być traktowany jako odcinek prostej. Jak wiadomo, we Wszechświecie prostych nie ma, wszystkie przestrzenie są „krzywe”, a zatem proste i odcinki prostych też są zakrzywione. Najmniejszą odległość między dwoma punktami w przestrzeni kosmicznej wyznaczają odcinki linii geodezyjnych.

Odstęp r₀ jest więc sumą odcinków geodezyjnych: kołowej (lub ogólniej eliptycznej dla cząstki elksjomaterialnej) i hiperbolicznej dla cząstki sprochnomaterialnej.

1.7 Składniki Wszechświata.

1.7.1 Składniki materialne.

W powszechnym mniemaniu Wszechświat zawiera tylko jeden rodzaj materii, czyli ten, z której jesteśmy uformowani, a także z której utworzone jest wszystko, co nas otacza. Nauka idzie trochę dalej: rozróżnia „materię zwykłą”, nazywaną niekiedy w publikacjach naukowych z grecka koinomaterią, oraz „antymaterię”, symetryczną wobec zwykłej przez to, że tam gdzie w materii zwykłej występują ładunki elektrostatyczne ujemne, w antymaterii mają one znak dodatni, i na odwrót. Przeciwnego znaku są także inne liczby kwantowe. Masy cząstek obu kategorii pozostają niezmienione. W ten sposób w Modelu Standardowym znalazły się na trwałe antyprotony (ujemne) oraz antyelektrony (dodatnie) i wszystkie inne (z wyjątkiem antyfotonów) cząstki elementarne.

W tym miejscu muszę jednak zdradzić swój niepokój, odczuwany od dawna, o nazewnictwo antyelektronów. Nauka operuje obecnie dwoma terminami: pozytony i pozytrony, i jakoś nie może zdecydować się na jeden z nich. Taka trójznaczność: pozyton, pozytron, antyelektron, nie przystoi literaturze naukowej. Można domniemywać, że jeśli trwa to już ok. 80 lat, to w stosowanym nazewnictwie kryje się jakiś fałsz, przechodzący z pokolenia na pokolenie. Przyroda w najszerszym tego słowa znaczeniu ma tajemniczą zdolność samooczyszczania się z kłamstwa. Doświadczyli tego liczni „zbawiciele świata”, niestety bez potrzebnej autorefleksji.

Istotą mojej hipotezy jest twierdzenie, że ani pozyton, ani pozytron nie są antyelektronami, czyli nie wchodzą w znaczeniowy zakres antymaterii. A więc czym są?

Nie wiem. Być może są cząstkami materii zwykłej, ale z niewiadomych powodów występującymi we Wszechświecie w śladowych ilościach. Tak jak antycząstki pozyton/pozytron w spotkaniu z elektronem ulegają wspólnie anihilacji, czyli utracie ładunków (co jest oczywiste) i zamianie ich mas na energię dwóch fotonów gamma. Być może należą do kategorii cząstek zwanych przez naukę egzotycznymi, które można wytworzyć „sztucznie” w zderzaczach wystarczająco wielkiej mocy. W końcu w chemii istnieje precedens tablicy okresowej, zawierającej dane 118 pierwiastków, a być może już więcej, z których istnienie w Przyrodzie stwierdzono w liczbie nie większej niż 100. Pozostałe można wytworzyć sztucznie, jest to znów sprawa dysponowanej mocy i technologii.

Nie wdając się w polemikę na temat nieszczęsnych pozytonów/pozytronów, w dalszej części tego opisu przez antymaterię będę rozumiał:

materię o grawitacji dodatniej i ładunkach elektrostatycznych oraz innych podstawowych liczbach kwantowych przeciwnych co do znaku i kierunku w porównaniu z tymi danymi dla materii zwykłej,
materię, której cząstki elementarne wraz z ich fotonami są obecne w niedostępnej dla nas bezpośrednio pragmacie wyróżnionej stygmatami czasu kwantowego przeciwnymi (czyli odwróconymi o 180⁰) w stosunku do stygmatów, jakimi jest naznaczona materia zwykła, zaliczająca nas do pragmaty doświadczanej przez nas na co dzień.

Tak więc mamy już dwa składniki Wszechświata, które z racji ich przymiotów wygodnie byłoby nazwać jednym terminem. Najważniejsza jest wspólna grawitacja przyciągająca i dlatego proponuję nazwę elksjomateria (z greckiego elksi – przyciąganie).

Już chyba łatwo się domyśleć, że pozostałe dwa składniki materialne Wszechświata to dwie materie o grawitacji ujemnej. Są one zbiorami cząstek, o których właściwie nic nie wiadomo. Z klasycznej teorii Wielkiego Wybuchu dowiadujemy się, że erupcja protogwiazdy musiała zawierać również monopole magnetyczne, czyli wyizolowane bieguny magnetyczne, prawdopodobnie (to mój domysł, bo nigdzie nie znalazłem takiego potwierdzenia) dwojakiego znaku ładunków magnetycznych, np. N i S, zgodnie z tym, czego uczono nas w szkole na temat magnesów. Cząstki te są zapewne nieredukowalne, bo na złożoną budowę nie pozwalałyby siły grawitacyjnego odpychania. Tak sądzono, ale przecież podobna sytuacja ma miejsce w przypadku kwarków, o czym już wspominałem. Siła odpychająca kwarki rośnie z kwadratem ich odległości, a więc być może kwarki są analogiem omawianych monopoli?

Wszystko to wymaga nazwania, inaczej łatwo się w tym pogubić. Podobnie do poprzedniego amatorskiego słowotwórstwa proponuję dla omawianych dwóch rodzajów materii nazwę sprochnomateria (z greckiego sprochno – odpychać), natomiast ładunki o ujemnym znaku grawitacji nazwę sprochnonami. Żeby uniknąć konieczności używania przedrostka anty-, będę stosował dodatkowe oznaczenie materii i ładunków literami N (biegun „północny”) i S (biegun „południowy”). Komuś, kto zamierzałby przeprowadzać analizę wektorową sił magnetycznych, przypominam, że ładunki N emitują pole o zwrotach „wychodzących”, a ładunki S o zwrotach „przychodzących”, podobnie jak to jest w przypadku ładunków elektrostatycznych plus i minus.

Na ilustracji 5 (brak ilustracji w materiałach – przyp. red.) przedstawiam zaproponowaną systematykę materii Wszechświata. Czy jest ona kompletna? Odpowiadam: nie. Przede wszystkim można się zastanawiać, gdzie przyporządkować cząstki materii w ogóle pozbawione grawitacji? Naukowiec będzie miał na myśli przede wszystkim fotony, rzekomo pozbawione masy. Otóż ja mam duże wątpliwości, czy fotony nie mają masy, a jeżeli mają nawet znikomą, np. kilkanaście rzędów wielkości mniejszą od 1 eV, to nie ma jeszcze dostatecznego powodu, żeby je uznać za cząstki bezmasowe i neutralne grawitacyjnie.

No i wreszcie, czy Wszechświat naprawdę zawiera tylko te cztery składniki, o których napisałem? Tym razem jestem bardziej zdecydowany w odpowiedzi: jest jeszcze piąty składnik, bez którego nie moglibyśmy marzyć o samoregulującym i powielającym się Wszechświecie, a przede wszystkim o jakiejkolwiek „duchowości” materii, a więc także naszej, istot obdarzonych świadomością.

Tym składnikiem jest informacja. Istnieją poważne powody, żeby ten składnik potraktować oddzielnie.

1.7.2 Informacja. (Współ)uwikłanie cząstek i systemów kwantowych.

To już drugi kosmologiczny byt, którego nie daje się na razie jednoznacznie zdefiniować. Pierwszym była, przypominam, rzeczywistość. Z rzeczywistością sprawa była jednak nieco prostsza, tradycyjny termin kojarzył się bardziej znajomo, nadanie odmiennej nazwy dla potrzeb wyłącznie kosmologicznych było może mało eleganckie, ale mam nadzieję skuteczne. W przypadku rzeczywistości próbę wyjaśnienia tego pojęcia podjął wielki umysł Sir Rogera Penrose’a, natomiast z informacją zmierzył się autorytet Jamesa Gleicka w podobnie obszernym dziele Informacja (462 strony, Wydawnictwo Znak, Kraków 2012, w przekładzie p. Grzegorza Siwka).

Z informacją mamy do czynienia codziennie, informacja kolejowa, internetowa, meteorologiczna, pokątna, tajna, państwowa, czyli „służby” (nie codziennie) i dziesiątki innych form informacji. Jakie można tu mieć wątpliwości? I rzeczywiście przez dziesiątki lat nowoczesnej fizyki tych wątpliwości jakby nie było, tym bardziej że istniały zadomowione takie terminy zastępcze, jak biblijne Słowo, idea, wiadomość, powiadamianie, doniesienie, zawiadomienie, pogłoska i inne o zróżnicowanych znaczeniach sytuacyjnych. Ten spokój został zakłócony dopiero w latach 40-tych XX wieku przez matematyka Claude’a Schannona i wprowadzenie przezeń do obiegu pojęcia bitu jako jednostki miary informacji. Po odkryciu zjawiska splątania kwantowego cząstek i stanów kwantowych (quantum entaglement) sprawa została przesądzona: nic nie jest lokalne, w przypadku kwantowego splątania cząstek lub całych systemów ich właściwości pozostają w tajemniczy sposób skorelowane nawet wtedy, gdy te obiekty są oddalone od siebie o miliony lat świetlnych. Ten fenomen pod nazwą splątania kwantowego zajmuje poczesne miejsce w fizyce kwantowej i doczekał się obszernej literatury matematycznej i doświadczalnej, powodując, że na sceny naukowego dyskursu musiała wtargnąć informacja jako byt fizyczny, choć ciągle zagadkowy. Nie mogę w tym miejscu nie wspomnieć o historycznym i jak dotąd decydującym eksperymencie według pomysłu i pod kierownictwem francuskiego badacza Alaina Aspecta w 1982 roku. Pisze o tym autorytet nauki i literatury popularnonaukowej John Gribbin w książce Kubity i kot Schroedingera. W polskim przekładzie p. Marka Krośniaka (Prószyński, 2015) brzmi to następująco:

… eksperyment Aspecta wywołał znacznie większy oddźwięk niż eksperymenty pierwszej generacji i rok 1982 uważany jest za przełomowy (omalże rok zero współczesnej teorii kwantowej), w którym, jeśli chodzi o mechanikę kwantową, zmieniło się wszystko.

W niniejszej pracy nie mogę ściśle opierać się na teorii naukowej, dotyczącej splątania kwantowego, ponieważ moja ograniczona wiedza do tego mnie nie upoważnia, a ponadto niektóre aspekty tego zjawiska są ściśle powiązane z fundamentalnym w termodynamice i w kosmologii pojęciem entropii, które zamierzam znacząco rozszerzyć i spodziewam się, że przy okazji naruszę to, co nauka uznała za wystarczająco udowodnione. Z tego względu opisywane tu zjawisko zdalnej korelacji będę nazywał odmiennie, jako współuwikłanie kwantowe (sugestia Jamesa Glicka) albo krócej uwikłanie kwantowe. W zastosowaniu do niniejszego opracowania uwikłanie kwantowe zostanie zademonstrowane w Części II. Na razie wracam do informacji.

Informacja okazuje się bytem niezniszczalnym. Wiele lat trwała wokół tego zażarta dyskusja między wybitnymi fizykami. Stephen Hawking twierdził, że informacja, która znalazła się wraz z materią wewnątrz czarnej dziury, ulega wraz z nią całkowitemu zniszczeniu. Jego oponentami byli Leonard Susskind (Stanford University) oraz Gerard t’Hooft , noblista z uniwersytetu w Utrechcie. Prace teoretyczne, również samego Hawkinga, potwierdziły po latach, że, tak jak energia, informacja generowana przez jakąkolwiek masę lub promieniowanie jest niezniszczalna, czyli „zachowana”. Spór zaowocował świetną książką Susskinda pod polskim tytułem Bitwa o czarne dziury (przekład Urszula i Mariusz Seweryńscy, Prószyński, 2011), na którą nieraz jeszcze będę się powoływał.

I na tym właściwie kończy się moja „niby naukowa” znajomość przedmiotu. Odnoszę jednak wrażenie, że od zakończenia „Bitwy” nauka nie posunęła problemu spektakularnie do przodu.

A zatem dalej będę posługiwał się tylko swoją wyobraźnią i intuicją.

Informacja w mojej hipotezie kosmologicznej będzie dotyczyć wszystkich parametrów, jakie opisują bieżący (chwilowy) stan kwantowy każdego bytu fizycznego. Podobnie do elektrostatyki, magnetyzmu i grawitacji, informację traktuję jako kwant ładunku, ładunku informacyjnego. Chciałoby się, żeby te ładunki nazwać „po znajomości” bitami. Nic z tego, już pisałem, że systemy dwójkowe nie mogą wchodzić do systemu liczbowego Wszechświata. Nauka też to wie i jeszcze więcej, dlatego wymyślono jednostkę miary nazwaną kubitem (qbit, q-bit), który powinien być więcej niż dwuwymiarowy. Nie mając dostatecznej wiedzy o kubitach, tworzę na użytek jedynie niniejszej hipotezy jednostkę elementarną informacji kosmologicznej pod nazwą informon. Informony nie mają masy i właściwości charakteryzujących stany kwantowe materii. Mają tylko treść (content) i podobnie jak kwarki nie występują swobodnie, lecz są integralnie związane ze swoimi „nośnikami”, materialnymi lub polowymi, z którymi są związane jakby w biologicznej symbiozie. Można sobie wyobrazić taki nośnik jako cienką otoczkę na zewnętrznej powierzchni cząstki. Otoczka z czego? Inne pytanie, jakie się tu narzuca: a informon jest jednostką (kwantem, najmniejszą porcją) czego, skoro nie materii? Jak wyobrazić sobie najmniejszą porcję czegoś tak nieuchwytnego, jak treść, i czy w ogóle jest to możliwe? To ostatnie pytanie można skomentować krótko: skoro autor baśni ma kłopot z wyobrażeniem sobie opisywanego przezeń zjawiska, to jeszcze wcale nie znaczy to, że nie potrafią tego uczynić jego czytelnicy.

Wspomniałem już w rozdziale o przestrzeni i nadprzestrzeni o istnieniu dwóch pól „kosmogonicznych”, czyli pierwotnych, stanowiących wylęgarnię wszechświatów. Jedno z nich, pole informacyjne, oznaczane przeze mnie grecką literą psi (Ψ), jest kwantowym nośnikiem wszelkiej informacji. Można sobie wyobrazić ten nośnik w postaci idealnej geometrycznie wielooczkowej pajęczyny powlekającej całą nadprzestrzeń, każdą cząstkę materialną, elementarną lub tworzącą z innymi złożony układ kwantowy. Te oczka mogą być niezajęte i pozostają wtedy kwantami pola Ψ, i mogą być zapełnione przez informony i stanowić część pamięci Wszechświata. Tak, zdecydowanie potwierdzam to, co napisałem: Wszechświat, a może inne wszechświaty również, mają swoją niezniszczalną pamięć cyfrową o nieznanych (na razie?) kodach. Przyjęcie tego stwierdzenia do wiadomości warunkuje możliwość akceptacji dalszego wywodu.

Tu niezbędne jest pewne zastrzeżenie: porównanie otoczek z pajęczyną sugeruje, że są one tworami dwuwymiarowymi. Wprawdzie pajęczyny mają swoją grubość, a więc są trójwymiarowe, niemniej jednak analogia jest zbyt sugestywna. Piszę otwarcie: na razie nie mam żadnych podstaw do twierdzenia, że otoczki z pola Ψ są dwuwymiarowe albo trójwymiarowe. Leonard Susskind w przywoływanej już książce Bitwa o czarne dziury twierdzi, że grubość powłoki (którą za innymi autorami nazywa rozciągniętym horyzontem (stretched horizon) jest równa długości Plancka, czyli 1,61624 x 10^-35 m. Sprawa wymaga jednak głębszego przemyślenia. Dodam tylko, że nazwa „rozciągnięty horyzont” nie bardzo mi się podoba. Autorzy, na których powołuje się Susskind, nie wymieniając zresztą ich nazwisk, powodowali się prawdopodobnie tym, że omawiany horyzont jest jakby naciągnięty (jak skarpetka na stopę) na każdy obiekt materialny. Proszę nie mylić tego horyzontu z horyzontem zdarzeń (event horizon) w fizyce czarnych dziur, będącym obiektem wirtualnym. Osobiście wolę nazwę „horyzont informacyjny” i takiego terminu będę używał. Autor Bitwy o czarne dziury twierdzi, że stretched horizon jest obecnie standardowym terminem w fizyce czarnych dziur (?), więc przy nim zamiennie pozostanę, co niekiedy może być powodem wątpliwości, które jednak będę od razu wyjaśniał. Wiele terminów w tej książce musiałem stworzyć ad hoc, z czym wiąże się pewna odpowiedzialność. Nauka obfituje w terminy poczęte właśnie w podobnych warunkach, tyle że ich autorami byli zwykle uznani fizycy i przez szacunek dla nich pozostały. Często ze szkodą dla nauki. Tworzona na bieżąco otoczka pamięci cząstki materii, w miarę wzrostu złożoności układu cząstek związanych ze sobą uwikłaniem kwantowym, zamienia się w otoczkę całego układu takich cząstek na zasadzie hierarchicznej. Polega to na tym, że informacja pochodząca od cząstki lub układu stojących na niższym szczeblu ewolucji staje się „automatycznie” częścią zewnętrznej otoczki układu, spełniającej teraz rolę nośnika dla informonów całego układu, będącego kolejnym krokiem ewolucji. Przypomina to trochę rejestry pamięci procesorów. Nośniki informonów przesuwają więc informację na coraz wyższy poziom ewolucji, aż do osiągnięcia umownego jej (ewolucji) kresu. Tym „kresem” może być, jak później pokażę, zakończenie kolejnego cyklu ewolucji wielowszechświata. Nie jest to równoznaczne ze zniszczeniem całej informacji po zakończonym cyklu, ponieważ jest ona, tak jak energia, niezniszczalna. Jej dalszy los może się wydać pasjonujący i poświęcę mu oddzielne miejsce.

Jeszcze na koniec tego rozdziału uwaga usprawiedliwiająca. Dobrze zdaję sobie sprawę z tego, do jakiego chaosu terminologicznego doprowadziłem. Są to terminy tworzone naprędce, w miarę potrzeby i w żadnym wypadku nie mam ambicji do ich utrwalania. Po prostu musiałem to robić, bo byty, do których się odnoszą, formalnie nie istnieją, a przynajmniej nie są mi znane zarówno z literatury popularnonaukowej, jak i fantastycznonaukowej.

1.7.3 Informacja, a energia.

Co może mieć wspólnego informacja z energią? Jest przecież „tylko” treścią, i gdyby nawet ta treść była bardzo pochlebna, np. dla dostawców energii elektrycznej, to przecież nie miałoby to żadnego wpływu na obniżenie wysokości płaconego rachunku. W odwrotnym wypadku jednak nie ręczę, rachunki mogą wzrosnąć. To nie jest tylko kiepski żart. Chcę tu utwierdzić przekonanie, że w bilansie energetycznym informacji należałoby uwzględnić także niebagatelne środki materialne i mentalne na zabezpieczenie treści przed jej nieautoryzowanym wykorzystaniem albo uszkodzeniem. Nie wiem, czy Wszechświat zabezpiecza swoją informację przed jej uszkodzeniami. Jestem zdania, że raczej tak, ale przy dzisiejszych środkach technologicznych nie można jeszcze badać systemu (lub systemów) kodowania informacji kosmologicznej.

Na zaprojektowanie i wyprodukowanie kostki pamięci, niezależnie od technologii, trzeba zużyć niemało energii, i jej koszty są „zaklęte” w cenie kostki. W trakcie użytkowania tej kostki trzeba jej dostarczać zasilanie elektryczne albo inne, bez tego jest martwa. No i najważniejsze: zapamiętana informacja do czegoś służy i musi być przemieszczana do innych nośników oraz na nich zakodowana i zapisana, a to nie odbywa się za darmo, wymaga energii.

Energia potrzebna do jej przetransportowania z jednego nośnika na inny. Niekiedy tam i z powrotem. Środkiem transportowym są infofotony (lub krócej infony), czyli nadświetlne fotony, których zadaniem jest przenoszenie kwantów informacji na zewnętrzną powierzchnię horyzontu. Poza ogromną prędkością różnią się od zwykłych („einsteinowskich”) fotonów tym, że nie są, jak zapewne kwalifikowałaby je nauka, bozonami. Nie przenoszą „oddziaływań”, ale przenoszą informację. STW czegoś takiego nie przewidywała, wprawdzie już wtedy, 100 lat temu, sporo wiedziano o czarnych dziurach, ale nie o tym, że wewnątrz nich została uwięziona potężna informacja, którą trzeba natychmiast i z ogromną szybkością z nich „ewakuować”, nawet na przekór szczególnej teorii względności. A jeśli nie, to co? Nic specjalnego: po prostu nasz Wszechświat nie przeżyłby nawet fazy inflacji kosmologicznej Alana Gutha, czyli ok. 10^-32s.
Energia (jeśli taka jest potrzebna) skwantowania i zakodowania informacji, a właściwie jej treści. Proszę o rozróżnienie „informacji” jako realnie istniejącego bytu fizycznego, mającego w tej opowieści swój równoważnik energetyczny, od jej zawartości treściowej, w literaturze anglojęzycznej określanej słowem „content”. We współczesnej literaturze kosmologicznej nie napotkałem takiego rozróżnienia semantycznego, stąd powyższa uwaga wydaje się niezbędna.

Przyznaję się otwarcie: nie wiem, czy ta faza przygotowania informonów do „podróży” w ogóle wymaga energii materialnej lub innej. Sądzę, że ta faza mieści się w ramach procesu kwantyzacji informacji, o ile taki proces w ogóle zachodził i zachodzi. Bardziej prawdopodobne wydaje się, że przyrodzoną postacią informacji jest postać dyskretna, może nawet cyfrowa, natomiast jej forma analogowa wytworzyła się w ciągu ewolucji gatunków, jako jeszcze jeden środek ich bezpieczeństwa. Jeżeli jednak o takiej energii tu wspominam, mimo że moja wyobraźnia w tym miejscu odmawia mi współpracy, to tylko po to, żeby do znudzenia przypominać, że w Kosmosie rachunek wydatków energetycznych jest niezwykle skrupulatnie kontrolowany i żadne niedomówienia na nic się nie zdadzą. Piszę tylko o rachunku wydatków, bo z przychodami sprawa jest „prosta”: Wszechświat, a nawet cała „rodzina wszechświatów”, czyli multiwszechświat, jak to w szerszym znaczeniu nazywa John Gribbin, badacz i autor znakomitych książek, otrzymują w procesie „proto konwersji (czyli zjawiska znanego nauce jako „wielki wybuch” lub „wielkie odbicie”) jednorazowy zastrzyk energii, który musi mu wystarczyć na całe jego trwanie i ewoluowanie. I tu, niestety, moja wyobraźnia jest stanowcza: więcej z protogwiazdy lub, jak niekiedy chce nauka, z „osobliwości” nie da się wycisnąć. Zasada minimalizacji „energii zużycia” jest, obok zasad ortogonalności, współuwikłania i symetrii, kardynalną w tej opowieści.

No dobrze, ale jeśli jednak tej energii nie starczy, bo pojawiło się „przypadkiem” zbyt dużo tzw. patologicznych czarnych dziur, czyli takich, w których nie następuje metatropia (z gr. μετατροπη, metatropi – konwersja, przemiana) czterech rodzajów materii, a jedynie pochłanianie i spalanie tego, co wpadło w procesie akrecji do środka tej „dziury”? Po prostu Wszechświat na jakiś czas ewolucji utraci idealną symetrię i ortogonalność, aby wkrótce je odzyskać, oczywiście kosztem utraty (czyli przemiany na ciepło i jej rozproszenia) niezbędnej do tego energii. Jeśliby tego nie zrobił, szybciej ulegnie kosmo-agonii, czyli samoanihilacji. Powrócę do tej kwestii w rozdziale 9. Termin kosmoagonia nie jest spotykany w kosmologii akademickiej, roszczę więc sobie prawo do jego autorstwa na użytek tego opracowania.

Obie wymienione kilka akapitów wcześniej energie 1) i 2) skutkują tym, że każdemu przekroczeniu przez infofotony horyzontów (zdarzeń lub informacyjnego) towarzyszy wysoka temperatura, co zostało potwierdzone przez astrofizyków doświadczalnych i co jest gołym okiem widoczne na mapach Plancka. Postaram się to jeszcze pokazać graficznie w części II.

Nasuwa się pytanie: czy udział tych energii transportu i zapisu da się ocenić ilościowo?

Odpowiedź w ramach niniejszej opowieści jest pozytywna, sama Natura oraz towarzyszący jej system liczbowy wydają się na to pozwalać. Zwróćmy uwagę na to, że infofotony z informonami na karku muszą pokonać niezmiernie krótką i niezmienną drogę, równą długości Plancka wewnątrz horyzontu, oraz drugą taką samą po stronie zewnętrznej tego horyzontu. Energetycznie liczy się ta druga trasa, bo po jej pokonaniu infofotony muszą pozbyć się swojego ładunku i powrócić tam, skąd przybyły, czyli powtórnie przekroczyć horyzont, tracąc ponownie część swojej energii. Jest to opis bardzo uproszczony, sporządzony na bazie fizyki klasycznej, co może ułatwić zrozumienie istoty opisanego procesu. Oczywiście nie ma tu miejsca na jakiś ruch infofotonów, „pokonywanie trasy” czy „zrzucanie ładunku”. Powracając na łono fizyki kwantowej, musimy zastąpić te określenia „probabilistycznym stawaniem się”. Jeżeli ten opis jest słuszny, to obliczenie kosztów energetycznych całego procesu okazuje się łatwe. Dlaczego? Bo z tego opisu można wyciągnąć wniosek, że te energetyczne koszty są znormalizowane, to znaczy, jeżeli je odnieść do energii „wejściowej”, czyli tej na wstępie procesu, to wyrażą się taką samą zależnością matematyczną.

Jeszcze jedna bardzo istotna uwaga, która będzie rozwinięta w części II: w pewnych okolicznościach infofotony nie wracają „tam, skąd przybyły”, jak napisałem wyżej, i pozostają na zewnątrz horyzontu. Po co, jaka ich tam czeka rola, a zwłaszcza jaka jest ich szybkość, skoro przekraczają horyzonty bez oglądania się na tzw. stożki światła w czasoprzestrzeni Minkowskiego? Proszę o cierpliwość.

Przypomnę teraz kilka właściwości liczby Φ, jedynie te, które będą konieczne dla jaśniejszego dalszego wywodu.

Φ –Φ^-1 = 1 (tu i dalej chodzi oczywiście o jedynki kosmologiczne)
Φ + 1 = Φ²
Φ^-1 + Φ^-2 = 1
Φ^-1 = Φ^-2 + Φ^-3_{a zatem}
Φ^-3 + 2x Φ^-2 = 1

Jeżeli przypisywać jedynce właściwości jakiejś kompletności (np. energii), kuszące jest, żeby w równaniu (5) liczbie Φ^-3 przypisać energię zawartą w treści informacji, a w podwojonej liczbie Φ^-2 energię całej pozostałej materii według znanego i często nadużywanego wzoru E = m x c². Ta pokusa nie wzięła się znikąd, poprzedził ją długi ciąg rozważań i obliczeń, które nie mają tutaj znaczenia, są po prostu niekiedy oparte na zbyt słabych przesłankach i nadmiernej intuicji.

Niestety, tylko pierwsza część zdania na początku akapitu okaże się trafna, poparta obserwacjami przywołanymi w dalszej części. Całe zdanie oparte na równaniach matematyki i fizyki klasycznej prowadzi na manowce. Matematyka Wszechświata uznaje tylko sumy i różnice zdefiniowane w algebrze Boole’a, a nie działania arytmetyki klasycznej.

Na użytek niniejszej hipotezy proponuję następujący wzór na energię kwantu informacji, jako „równoważną” zawartej w niej treści:

dla przypadku, kiedy infofotony po przeniesieniu informacji na zewnątrz horyzontu wracają do jego wnętrza, oraz:

dla przypadku infofotonów pozostających na zewnątrz horyzontu po wykonaniu zadania transportu informacji. Jak widać, każdorazowe przekroczenie powierzchni horyzontu przez nieuwikłane ze sobą infofotony wiąże się nieuchronnie ze stratą ich energii (czyli zmniejszeniem częstotliwości) o czynnik Φ-1.

Jestem przekonany, że w tym miejscu pojawią się nowe wątpliwości wobec tak arbitralnego sformułowania równań (6) i (7). Będę próbował je rozwiać w następnych rozdziałach. Na razie wspomnę, że treść informacji opisująca stany kwantowe cząstek lub ich układów wiąże się ściśle z pojęciem naukowej entropii i każdorazowa zmiana „uporządkowania” materii wiąże się z wydatkiem lub poborem energii. Sprawa jest delikatna, bo według nauki nie można mieć wpływu na proces nieustannego wzrostu entropii Wszechświata, a więc zmiana energii jest jednokierunkowa.

Ilościowa trafność podanych wzorów będzie mogła być uzasadniona dalej, przy opisywaniu istoty tzw. stałej struktury subtelnej (SSS).

1.7.4 Informacja, a Piękno i Sztuka.

Muszę jeszcze raz powrócić, choćby bardzo skrótowo, do wcześniej wspomnianych wątpliwości i refleksji związanych z dekodowaniem informacji kosmicznej (nie nazywam jej kosmologiczną, bo w nauce, jaką jest kosmologia, takiego pojęcia nie ma, funkcjonuje natomiast „zdalne oddziaływanie”). Czy istnieje możliwość dekodowania tej informacji, czy nie istnieje? Jeśli istnieje, to czy mamy szanse na jej zdekodowanie w nawet odległej przyszłości, np. za pomocą komputerów kwantowych o prędkości nadświetlnej? A może już od dawna korzystamy z takiej zdekodowanej przez nas, ludzi, informacji, nie zdając sobie z tego sprawy? A może nie w fizyce, nie w kosmologii trzeba szukać odpowiedzi na postawione pytanie? Czy spontaniczne dzieło artysty, w którym nie bardzo można rozróżnić dzieło i jego twórcę, nie jest właśnie efektem zdekodowania informacji kosmicznej bez udziału świadomości artysty? Realności takiemu pomysłowi dodaje uzasadnione przypuszczenie, że „artystyczne” zdekodowanie informacji kosmicznej skutkuje następnie jej indywidualnym przetworzeniem albo uzupełnieniem przez artystę, czego wynikiem może niekiedy być nieśmiertelne dzieło sztuki albo, niestety, nieśmiertelny kicz.

Takie refleksje i pomysły narzucają się przede wszystkim w odniesieniu do muzyki. Po pierwsze dlatego, że proces jej komponowania na wiele instrumentów lub głosów, np. symfonii lub opery, właściwie jest czymś niepojętym, zdaje się także dla samych kompozytorów, o czym będzie dalej. Po drugie, efekt tego tworzenia może być lub nawet musi być natychmiast zapisany w niedostępnym dla zwykłego odbiorcy szyfrze, jakim jest zapis nutowy lub inny, może pamięciowy? Mało tego: mój przyjaciel, znawca tej dziedziny sztuki, powiedział mi, że niektóre utwory Bacha lub raczej ich fragmenty udało się teoretykom muzyki zapisać jako ciągi cyfr i liczb, co by znaczyło, że muzyka jest „matematyczna z natury”. A jeśli muzyka, to chyba inne rodzaje Sztuki także? Dlaczego miałaby być wyjątkiem? Pytania można mnożyć bez końca.

To, co wyżej napisałem, nie jest tylko moim dylematem i powodem do fantazjowania. Sięgam choćby po powieść mojego ulubionego pisarza izraelskiego Amosa Oza Dotknij wiatru, dotknij wody, w przekładzie pani Danuty Sękalskiej (wyd. Muza, 1998). Jeden z bohaterów powieści, nie naukowiec, przewodniczący kibucu w północnej Galilei, tak notuje swoje przemyślenia fizyko-muzyczne w prowadzonym przez siebie dzienniku:

…Masa. Energia. Elektryczność. Pole magnetyczne. Z drugiej strony: Czas. Przestrzeń. Ruch. A także: Wola. Cierpienie. Jeżeli to wszystko ma jakiś >>punkt styczny<< lub >>klamrę<< – to jest to muzyka.

I dalej: Mamy zatem przed sobą skalę muzyczną. Odtąd czas i wola, elektryczność i obraz, przestrzeń, magnetyzm, cierpienie, grawitacja mogą być postrzegane synoptycznie, całościowo, w obrębie jednego systemu – tonacja, modulacja, rytm. Przeobrażenie czasu i materii. Dźwięczne skojarzenie subiektywnego z obiektywnym. Nazwijmy cały ten system „matemuzyką”.

Być może Amos Oz poszedł trochę za daleko przypisując, poprzez swego bohatera, wyłącznie muzyce rolę „klamry”, która integruje. Artyści innych dziedzin Sztuki mogą, jeśli się logicznie zastanowić, również „dekodować” informację o Pięknie, przekazywaną przez Wszechświat, a oni, artyści wszelkich sztuk, niezależnie od wykształcenia muzycznego i każdego innego, zostali być może obdarzeni szczególnymi narzędziami „matematycznymi”, niemieszczącymi się w świadomości, pozwalającymi na udostępnienie innym, nie tak ubogaconym, choćby okruchów zawartego w tej informacji Piękna? Jest wielce dla mnie zastanawiające, że są dzieła Sztuki, których odbiór bez udziału świadomości od razu przywołuje myśl o Kosmosie. W tej Opowieści nie powstrzymam się od zacytowania fragmentów dzieł z zakresu literatury pięknej i reportażowej. Zrobiłem to już na stronie tytułowej. (Chodzi o Wprowadzenie – przyp. red.) Nie ma na to miejsca w publikacjach stricte naukowych, w opowieściach jest.

No dobrze, ale kto skomponował dzieło Sztuki, zanim zostało ono zakodowane i utrwalone w nośnikach (infonach), a następnie zdekodowane przez wybrańców losu?

Czterotomowe dzieło polskiego pisarza Stanisława Vincenza (1888 – 1971) Na wysokiej połoninie (IW PAX, 1979), łączące w sobie najlepsze tradycje obu tych domen literatury, zawiera, wśród wielu innych, taką oto wypowiedź starego i chyba niepiśmiennego mieszkańca wieloetnicznej Huculszczyzny. Przytaczam ją, bo wydaje się być częściową odpowiedzią na wyżej postawione pytanie.

Stary „wieszczun gromowy”, odpędzacz burz i piorunów, mieszkający w samotnej chacie w karpackiej puszczy na stokach Czarnohory, gdzieś nad Czeremoszem, mówi:

Cały ten świat to wielka księga. A tamten świat i dusza człowiecza, to granie, muzyka. Widzący wieszczun męczy się, odgaduje, odczytuje, a niewidomy nawet nie potrzebuje tego i zna więcej, bo wszystko mu gra, wyśpiewuje samo.

Ten starzec wie, o czym mówi, to od wieków kraina ślepych lirników, wędrujących od sioła do sioła, jedynych łączników ze światem dla puszczańskich gazdów i pasterzy z połonin, ale także zbiegłych tam opryszków. Uległ czarowi tych ludowych rusińskich artystów Henryk Sienkiewicz i dał temu wyraz w Ogniem i mieczem.

Historia nauki oraz współczesna literatura popularnonaukowa zawierają bardzo liczne odniesienia do związku muzyki z Kosmosem. Określenie „muzyka sfer” sięga czasów Pitagorasa, Arystotelesa, Platona, a później Klaudiusza Ptolemeusza. Chodzi o kryształowe sfery, których doskonałość określona była i nadal jest mianem „brył platońskich” (znajdzie się dla nich miejsce w niniejszej opowieści), które kierowały ruchem ciał niebieskich. Temat tego związku jest wciąż aktualny, chociaż tak naprawdę nie bardzo wiadomo dlaczego. Mógłbym tutaj przytoczyć wiele cytatów z literatury pięknej i popularnonaukowej.

A co w tej sprawie twierdzi nauka?

Na pierwszy rzut oka może wydawać się, że nic. Problem wykracza poza zakres badań naukowych, a wchodzi w zakres badań metafizycznych, no i oczywiście staje się tematem dociekań pseudonaukowców, czego dowodem są te strony. Z tym większym zainteresowaniem sięgnąłem do książki wyjątkowej, prawdopodobnie jedynej na polskim rynku księgarskim, której autorem jest uznany fizyk, profesor amerykańskiego uniwersytetu, a jednocześnie profesjonalny jazzman nowojorski (saksofon) p. Stephon Alexander. Już po roku od pierwszego wydania The Jazz of Physics. The Secret Link Between Music and the Structure of the Universe (copyright 2016) ukazała się w polskim przekładzie p. Tomasza Krzysztonia (Prószyński, 2017) pod tytułem: Jazz i fizyka. Tajemniczy związek muzyki ze strukturą Wszechświata.

Jakkolwiek podtytuł dzieła obiecuje jakby trochę za dużo i chętnie widziałbym raczej słowo Sound zamiast Music, to jednak jest pewne, że autor dobrze wie, o czym pisze, nie tylko z powodu podwójnych hobbie i zawodu, ale również dlatego, że przytacza opinie muzyków będących idolami dla entuzjastów i znawców muzyki improwizowanej, wśród których się obracał i łączył obowiązki profesjonalnego badacza fizyka z pasją do muzyki jazzowej i teorią tej muzyki. Dla mnie najważniejsze okazały się opinie tych specjalistów na temat określony w podtytule dzieła. Możemy tam znaleźć także rozliczne przykłady związków znanych fizyków z czynnym uprawianiem muzyki, oczywiście z Einsteinem na czele, o czym donoszą również biografie Uczonego i pozostające po nim pamiątki. Niestety oczekiwania wyjaśnienia dosłownego znaczenia podtytułu byłyby przesadzone. Niech przykładem będzie cytowana przez p. Alexandra publiczna (w wywiadzie) wypowiedź kompozytora i pianisty Lennie’ego Tristano, znanego z „harmonicznego i improwizacyjnego podejścia do bebopu”, którą tak podsumował:

Ja niczego nie komponuję… Czy widzisz tę różnicę pomiędzy innymi gatunkami muzycznymi i jazzem? Muzyka już tkwi w twej głowie i wszystko, co musisz zrobić, to pozwolić rękom odtworzyć to, co słyszysz. Tak więc to, co otrzymujesz, jest czymś zupełnie spontanicznym.

Komentarz autora książki wyrażony został krótko:

Nie oszukujmy się, to nie jest takie proste. Szczególnie gdy chodzi o znaczenie słowa „spontaniczny” w kontekście improwizacji.

Musi zastanawiać zgodność poglądów niepiśmiennego „wieszczuna gromowego” z drugiej dekady XX wieku z nowojorskim, solidnie wykształconym muzykiem i naukowcem z pierwszej dekady XXI wieku co do tego, że muzyka do obu przychodzi z zewnątrz. Różnicy można się dopatrywać tylko w rozumieniu źródła ukrytej muzyki: dla pierwszego jest to otaczająca go Przyroda (a więc chyba także Kosmos?), dla drugiego, będącego również twórcą, doskonały i „spontanicznie” działający ludzki mózg, dyrygujący artystyczną inicjatywą twórcy.

Zastanawiające jest to, że w czasie kiedy powstaje ta opowieść, są artyści, którzy dostrzegając ten problem jako własny, intymny, zagadkowy, ale także ważny, godzą się w wywiadach o nim mówić. Przełamują skrępowanie, temat to przecież nad wyraz osobisty, ale jakby coraz częściej skłaniający wielu wybitnych twórców do otwartej refleksji. Przytoczę tylko jeden przykład, temat zbyt daleko odbiegł od głównego wątku. Oto wypowiedzi wybitnej pisarki, pani Olgi Tokarczuk, w wywiadach na temat Ksiąg Jakubowych:

…Towarzyszyło mi często uczucie, że oto złapałam koniec jakiejś nitki i posuwam się za nią, ufając, że to, czego szukam, zaraz wyłoni się przede mną zza rogu. I właśnie tak bywało. Nie wiem, czy w ogóle możliwe jest opisanie pewnego fenomenu, z którym miałam do czynienia wielokrotnie w czasie pisania, ale nigdy tak często i tak intensywnie jak przy tej książce. Więc chyba czas, żeby go nazwać. Spontanicznie i subiektywnie odbiera się to zjawisko tak, jakby jakieś zewnętrzne i niezależne siły zgłaszały swój akces do opisywanej historii, jakby sprzęgły się jakieś moce i niosły pomoc. OK, wiem, jak to brzmi. Odlotowo.

W takich sytuacjach człowiek zaczyna się najpierw podejrzliwie rozglądać dookoła, potem jednak przychodzi do głowy dziwaczna myśl, że z jakichś względów ś w i a t u z a l e ż y n a n a p i s a n i u t e j k s i ą ż k i. Zdaję sobie sprawę, jak niepoważnie to brzmi i jak bardzo stawia moją osobę w dwuznacznym świetle. Co mi tam! Pisarze są w końcu artystami, a artyści wywalczyli sobie większy margines ekscentryczności niż, powiedzmy, naukowcy, za co rezygnują z tytułów naukowych.

Żeby jednak dodać sobie powagi, ukułam dla siebie wsparcie w łacinie – taki pomocny świat, mundus adiumens, to coś, co niesie poczucie bycia prowadzonym za rękę i wprowadza w cudowny stan, podobny do narkotycznego transu, do lekkiej, całkiem przyjemnej i jednocześnie męczącej, z trudem opanowywanej psychozy. („Gazeta Wyborcza”, 28.12.2014 oraz 10–11.10.2015)

A zatem wracamy do punktu wyjścia. Pan Stephon Alexander nie daje jednak za wygraną i w znacznej części książki powołuje się na niezwykłą postać wykonawcy i teoretyka jazzu. Tą postacią był (zmarł w 1967 r.) John Coltrane. Entuzjaści jazzu w Polsce być może znają go z wielu płyt, ale p. Stephon skupia się przede wszystkim na Stellar Regions, Interstellar Space i Cosmic Sound. Nie mogę tu pomieścić wszystkich informacji, jakie przekazuje nam p. Alexander. W mojej ocenie droga badawcza Coltrane’a zmierzała najcelniej w kierunku, jaki, niezbyt udolnie, staram się zasugerować w tej książce. Ciekawostką może być, że wśród dorobku artystycznego i badawczego Coltrane’a znajduje się jego mandala, w której (podobnie do metody C.G. Junga, ale w znaczeniu bardziej matematycznym niż symbolicznym) chciał pomieścić najogólniejszą teorię muzyki. Alexander stwierdza, że odczytał ukrytą treść mandali i zestawia dorobek Coltrane’a z równaniami Einsteina, a właściwie niekończącymi się usiłowaniami ich unifikacji z czterema równaniami Maxwella w jedno ogólne.

Przyznaję, wiele tych informacji nie jestem w stanie zrozumieć, a tym bardziej przekazać. Z całym przekonaniem odsyłam zainteresowanych do wysłuchania wspomnianych wyżej płyt, są dostępne w Internecie, a także do bibliografii jazzu.

I jeszcze jedno, co mnie bardzo ucieszyło. W przedostatnim rozdziale swojej książki Autor dochodzi do bardzo ważnej konstatacji, którą muszę tu zacytować nie z powodu mojej próżności, ale dlatego, że przygotowuje ona ewentualnego Czytelnika do lepszego zrozumienia przestrzennych modeli Wielowszechświata i Wszechświata, jakie zademonstruję w dalszych częściach opowiadania. Oto, co pisze p. Stephon:

„Jeżeli na przykład nie istnieje nic na „zewnątrz” Wszechświata, a Wszechświat działa jak instrument, to instrument ten musi grać całym sobą. Innymi słowy, kosmiczny dźwięk to instrument, a instrument to kosmiczny dźwięk. Wszystko we Wszechświecie, łącznie z czasoprzestrzenią, musi drgać lub oscylować. I zaraz dalej: Jeśli tempo wykonuje oscylacje o częstości tonu czystego, to mamy to, co nazwałbym Wszechświatem lub, inaczej, cykliczną kosmologią”.

Moja opowieść snuje baśń o wszechświatach cyklicznych; gdyby aspirowała do rozprawy naukowej, trzeba by ją zaliczyć do literatury z zakresu kosmologii cyklicznej. W przeciwieństwie do wyobrażeń p. Alexandera ta cykliczność nie jest i nie będzie nieskończona. Ma swój początek i będzie miała swój koniec. Ale jest jeszcze coś, co tym razem jest „wieczne”. Tym czymś jest informacja. Jest niezniszczalna, zapisana pozostaje niezmienna. Proszę o uśmiech ulgi. Non omnis moriar!

Poświęciłem jakże ulotnemu tematowi Piękna i Sztuki w aspekcie informacji kosmicznej prawdopodobnie zbyt dużo miejsca w tej opowieści. Pragnąłem wszakże, aby pojęcie informacji jako realnego fizycznego bytu, równoprawnego z innymi postaciami energii, weszło choćby „ukradkiem” do indeksu wiedzy o fizyce, wszechświatach i o nas, istotach obdarzonych (przypadkiem?) świadomością. Z trochę utopijną nadzieją, że z upływem czasu stanie się to naturalnym przedmiotem i narzędziem badań naukowych, choćby z tego względu, że do Sztuki i jej Piękna należy zaliczyć także Poszukiwania Naukowe. Piszę to, nadużywając zapewne wielkich liter, ale pragnę przez to wyrazić, że w wielu obserwowanych przypadkach działania i dzieła ludzkie ocierają się o Absolut.

Po napisaniu tego podrozdziału spostrzegłem, że może on wywołać odczucie przypisywania przeze mnie artystom wyjątkowości pod każdym względem i to w aspekcie wyłącznie pozytywnym. Tak jak można (jeśli ktoś bardzo chce na osobisty użytek) „oceniać” Kosmos w aspekcie dobra i zła, tak samo można „oceniać” innych, będących „zespołem mikrocząstek” tego samego Kosmosu, a wśród nich także artystów. Od takiego poglądu już jest tylko krok do przypisywania Kosmosowi motywów wszelkiego działania istot obdarzonych świadomością. Bo, można dociekać, czy jest możliwe być mniejszym partnerem Wszechświata, a nie wyłącznie jego biernym niewolnikiem, cieszącym się, że dzisiaj był On dla nas łaskawy, ale jutro może nam pokazać swoją moc niszczycielską? Jakąś formą odpowiedzi na takie pytanie mogłoby być inne: no to jaka miałaby być rola świadomości?

Jest inna strona domniemanych „ludzi-dekoderów informacji kosmicznej”:

„Czy dzieła artysty są naznaczone jego osobistymi winami? Czy możemy szanować i podziwiać ludzi, którzy są wybitnymi artystami, ale brakuje im tego, co nazywamy zwykłą ludzką przyzwoitością?”, pyta dziennikarz „The Wall Street Journal”, p. Adam Kirsch (24.01.2019). I dalej: „ Oczywiście, nie tylko artyści – malarze, aktorzy czy pisarze – są przedmiotem bacznej uwagi ze strony społeczeństwa. Grzechy artystów spotykają się jednak z inną reakcją niż zło wyrządzone przez bankierów czy polityków. Nie czujemy żadnego duchowego pokrewieństwa z tymi drugimi – w przeciwieństwie do tych pierwszych – ani nie darzymy ich podobnym uwielbieniem, nie identyfikujemy się z nimi, nie są bohaterami masowej wyobraźni”. (Czy artyście wolno więcej?, tłum. Maciej Orłowski, WSJ, dodatek do „Gazety Wyborczej”, nr 8 (59)). Oto do jakich dociekań może doprowadzić częste spoglądanie na nocne sklepienie niebieskie!

1.8 Intropia.

1.8.1 Intropia. Podstawy.

Cóż to jest takiego, jeśli w ogóle jest? Nazwa kojarzy się z entropią, co może prowadzić do nieporozumień, przed czym przestrzegam. Brałem pod uwagę inne terminy, np. funkcja falowa, ale dopiero wtedy nastąpiłby chaos, jako że funkcja falowa wyodrębniona matematycznie przez Schroedingera jest czymś całkiem odmiennym, a spory fizyków o jej naturę trwały dziesiątki lat. Ale nie zmienia to faktu, że intropia, byt fizyczny, a więc także matematyczny, jest też funkcją i należy ją traktować, jako próbę powiązania ze sobą kilku innych bytów (raczej oddziaływań) z zakresu fizyki klasycznej.

Tymi bytami przede wszystkim są: grawitacja, przestrzenna „rozciągłość” rozpatrywanej materii i… entropia „bolzmanowska”, a właściwie tylko kierunek jej zmian w stronę stanu równowagi termodynamicznej, ale (koniecznie!) z uwzględnieniem obecności grawitacji, dodatniej bądź ujemnej. Jest to próba trochę szaleńcza, bo co innego oznacza odczuwać brak tego rodzaju matematycznego tworu, a co innego prawidłowo go sformułować. Już samo pojęcie „rozciągłości”, lub jej braku, użyte w cennym przekładzie Monadologii G.W. Leibniza przez Henryka Elzenberga (!), nie jest całkiem jasne (w oryginale franc. étendue i inétendue). Wolę pojęcie „rozległość”, bliższe temu, co chciałbym wyrazić słownie. W moim rozumieniu będzie to „gabaryt” granicznej powierzchni bryły, w której zamknięta jest cała rozpatrywana materia, będąca w stanie realnego rozproszenia we Wszechświecie, wymuszonego i ukształtowanego przez entropię, grawitację i jeszcze inne siły, o których wkrótce napiszę. Taka zamknięta w trójwymiarowej bryle intropii materia ma stałą gęstość prawdopodobieństwa napotkania cząstki w dowolnym miejscu bryły, podobnie do tzw. ”gęstości krytycznej” materii Wszechświata, ocenianej przez naukę na ok. 10^-30 g/cm³. To jedynie analogia, bo w istocie obie te gęstości niewiele mają ze sobą wspólnego, jedna pochodzi z probabilistcznej fizyki kwantowej, a druga z deterministycznej klasycznej. Tego rodzaju postępowanie jest oczywiście znacznym uproszczeniem i nie pretenduje do zobrazowania niesłychanie złożonej struktury Wszechświata, ale, jak każda rozsądna i świadoma interpolacja, pozwala na dostrzeżenie zaskakujących zbieżności, a także i rozbieżności, które można później konfrontować z aktualnymi stwierdzeniami nauki.

Niestety, kłopot na tym się nie kończy, bo oto intropia w procesie ewolucji Wszechświata „chce być” także falą, a więc do jej przedstawienia wkrada się jeszcze klasyczny czas. W takich przypadkach, chcąc uwydatnić jej falowość, będę ją nazywać falą intropową.

Wobec takich wątpliwości nasuwa się pytanie: po co w ogóle powoływać do użytku taką funkcjo-falę skoro są kłopoty z jej matematyczną formułą?

Przemawia za tym kilka powodów.

Najważniejszą dla mnie okazuje się konieczność graficznego przedstawiania tworzonych w wyobraźni zespołów materii i całego domniemanego na tej podstawie wnętrza Wszechświata. Dysponując odpowiednim programem graficznym 3D mogę temu programowi powierzyć zadanie matematycznego obliczania kształtu, a nawet animacji wyobrażonych brył i ich grup bez wnikania w aparat matematyczny, którego w niezbędnym zakresie nie znam. Te bryły i ich grupy to właśnie chwilowe stany intropii w dowolnej erze i fazie ewolucji, z udziałem wieloosiowej animacji lub bez niej. Problemem staje się wtedy raczej opanowanie możliwości programu 3D w takim stopniu, żeby chciał być posłuszny wyobraźni autora, a także żeby odbyło się to przy użyciu możliwie oszczędnej ilości danych, z którymi mój nieprofesjonalny laptop jeszcze będzie mógł sobie radzić. Uniknięcie intropii zmusiłoby do graficznej prezentacji zawartości Wszechświata osobno dla różnych oddziaływań, co uczyniłoby całą prezentację mało albo w ogóle nieczytelną.

Jest jednak jeszcze inna grupa powodów mających na celu skonfrontowanie uzyskanych wyników z tymi, jakie już zostały opublikowane w poważnej prasie popularnonaukowej i w monografiach naukowych, które otrzymano na odmiennych, bo naukowych, ścieżkach rozumowania, a także przy użyciu zdecydowanie wydajniejszych komputerów. Jest więc interesujące, do czego może doprowadzić tak bardzo amatorskie, nie naukowe rozumowanie i sprawdzenie, czy są w nim elementy nadające się do naukowego dyskursu. Czy rzeczywiście pogarda dla pseudonaukowych dociekań ambitnych „konsumentów nauki”, o których wspomniałem we Wprowadzeniu do tej opowieści jest w pełni uzasadniona? A może właśnie ona, ta pogarda, jest „nienaukowa”?

W przypadku intropii, funkcji powołanej przeze mnie ad hoc, jest to tym bardziej wskazane, ponieważ wydaje się, że uwzględnia znaczeniowo o wiele szerszy zakres oddziaływań fizycznych, niż klasyczne pojęcie entropii w termodynamice, o czym napiszę poniżej. Byłoby interesujące zestawienie ze sobą wyników możliwych do wykonania obliczeń, może z tego coś wynikać. To nie kosztuje, a w opowieści jest dopuszczalne.

Chciałbym oczywiście, żeby „moja” intropia była funkcją wystarczającą do opisu Wszechświata z dostateczną ścisłością, ale czy w ogóle taka możliwość istnieje? Jestem przekonany, że tak, ale nie sądzę, żeby mogło się to odbyć bez narzędzi zaawansowanej matematyki.

Należy wyodrębnić dwa rodzaje intropii:

a) intropię termodynamiczną, znaczeniowo najbliższą pojęciu entropii układu zamkniętego, oraz:

b) intropię informacyjną, uwzględniającą fakt zawartości informacyjnej rozpatrywanego układu, zamkniętego wewnątrz powierzchni jej horyzontu, zgodnie z zasadą holograficzną energicznie, podtrzymywaną przez Susskinda.

Jeśli przez

oznaczyć intropię termodynamiczną, a przez

intropię informacyjną, gdzie przez tę drugą będę rozumiał:

to intropia całkowita w notacji kosmologicznego systemu liczbowego będzie:

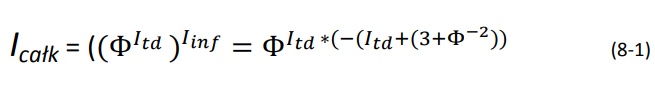
W tych równaniach rozpoznajemy obecność energii kwantu informacji według wzorów (6) i (7).

Silny związek intropii informacyjnej z termodynamiczną nie powinien dziwić: według naszej klasycznej logiki najpierw musi się coś dziać, żeby potem było o czym opowiadać. Odwrotna kolejność w Kosmosie nie wydaje się tolerowana. A jednak…

Czy naprawdę można uznać to stwierdzenie za jedną z zasad Wszechświata? A jeżeli znajdę w tej baśni choćby jeden przykład, że może być odwrotnie? Uważny czytelnik znajdzie taki przykład w części 3. Daję słowo!

Warto natomiast zwrócić uwagę na fakt, że obecność intropii informacyjnej zmienia znak całego wykładnika potęgowego w równaniu (8) na ujemny. Oznacza to, że Wszechświat od pewnej fazy ewolucji przestał się rozszerzać i zaczął się gwałtownie kurczyć, czyli w języku Leibniza i Elzenberga zmniejszać swoją rozciągłość. Jaka to faza, dowiemy się dalej. Na „pocieszenie” zauważmy, że całkowita intropia Wszechświata też się zaczęła zmniejszać, co oznacza, że obecna i czekająca nas przyszłość jest i będzie coraz bardziej „uporządkowana”. Kto lubi porządek powinien się cieszyć.

Intropia odgrywa zbyt ważną rolę w tej opowieści, by można było w tym miejscu zakończyć jej temat. Przerwę go tylko na krótko, bo rozwinięcie tego tematu w dalszej części będzie wymagało ujawnienia jeszcze innych „fundamentów” całej koncepcji.

1.8.2 Intropia. Historia ewolucji zawarta w długości Plancka.

Wartość liczbową długości Plancka, jednostki długości w układzie jednostek naturalnych, znamy już z rozdziału 2. Można ją wyrazić przez związek trzech innych stałych, a mianowicie (h/2π), G i c, według wzoru:

Niestety, już wcześniej wyraziłem wątpliwość, czy stałe G i c mogą być traktowane, jako niezmienne w toku ewolucji Wszechświata, co jawnie zaprzecza ustaleniom nauki. Traktuję więc wartość l_p, jako zmienną w toku ewolucji wielowszechświata, którego doświadczany przez nas Wszechświat jest zaledwie jednym z cykli ewolucyjnych. Pisząc tutaj o ewolucji, mam na myśli zmienność l_pod samego początku wielowszechświata, aż do „teraz”. Długość Plancka jest oczywiście jednostką długości w fizyce skali subatomowej, lecz z zastrzeżeniem: o znanej nam wartości może nią być jedynie „tu i teraz”.

Za takimi przypuszczeniami kryje się podejrzenie, że długość Plancka może zawierać ukrytą informację o zmienności intropii, czyli o zmianach stanu energetycznego wszystkich cykli ewolucyjnych Wszechświata, poczynając od początku cyklu 1-go… Te zmiany stanu możemy uznać za ubytki zasobów energetycznych i informacyjnych Wszechświata w miarę jego zbliżania do stanu równowagi termodynamicznej. Tu pojawia się istotny problem.

Jeżeli Wszechświat w każdym swoim cyklu, po „przeżyciu” etapu gwałtownej ekspansji zwanej przez naukę inflacją, zaprzestał dalszego wzrostu i zaczął się kurczyć, co z całym przekonaniem twierdzę, a nie nadal rozszerzać ( jak utrzymuje kosmologia akademicka), to zaczyna się kłopot ze znakami plus i minus.

Entropia naukowa w miarę zbliżania się do stanu równowagi termodynamicznej, równoznacznego z końcem istnienia Wszechświata, może być tylko dodatnia (wzrostowa) i niezmienna, nigdy ujemna (malejąca). Wszechświat, o którym piszę tę opowieść zachowuje się odwrotnie, po erze ekspansji zmierza do swojego kresu, kurcząc się. Uzasadnienie znajdzie się w oddzielnym rozdziale.

Możemy sobie z łatwością wyobrazić, że skoro doświadczamy długości Plancka o takiej wartości, jaką podaje CODATA, wyrażonej w metrach, to pierwotna protogwiazda w stanie startu do etapu kurczenia się, musiała także charakteryzować się „swoją długością Plancka” i ta długość była równa jednemu metrowi (oczywiście „kosmologicznemu”). To była wtedy najmniejsza możliwa długość, odległość lub rozległość, mająca „sens fizyczny”. Przecież tak właśnie nauka określa aktualną długość Plancka.

W mojej opowieści zrezygnowałem z pojęcia entropii na rzecz intropii, która uwzględnia w swojej semantyce wszelkie inne, nie tylko termodynamiczne, oddziaływania, o których coś wiemy, a także istnienie i skutki ilościowe istnienia informacji.

W miarę zbliżania się Wszechświata do stanu równowagi termodynamicznej, czyli (jak to się niekiedy określa) do „kolapsu”, intropia całkowita maleje, świadcząc w ten sposób, że zasoby energetyczne Wszechświata, nabyte wraz z narodzinami protogwiazdy, zużywają się. Intropia pozwala na ocenę utraty tych zasobów w poszczególnych cyklach ewolucji, a także w różnych fazach cyklu.

Jeśli tak miałoby być, to zgodnie z równaniem (8-1) w poprzednim podrozdziale, znaczyło by, że wykładnik potęgowy w zapisie Φ^{-166,476 3383}z rozdziału 2, powinien być iloczynem dwóch liczb, które oznaczę literami A i B. Ten iloczyn powinien być liczbą ujemną lub dodatnią, zależnie od tego, jaki kierunek ewolucji rozpatrujemy: czy z przeszłości do „teraz”, czy z „teraz” do domniemywanej przyszłości. Będziemy to jeszcze bliżej wyjaśniać. Oponentom, ekspertom z zakresu fizyki kwantowej, zwrócę uwagę, że pojęcie intropii należy do domeny fizyki klasycznej, w której przeszłość, teraźniejszość i przyszłość, i w ogóle czas, są terminami dopuszczalnymi.

Niech A oznacza wykładnik potęgowy intropii termodynamicznej, a B wykładnik potęgowy intropii informacyjnej.

Pojawia się tutaj nie pierwszy raz, problem terminologiczny. Liczby A i B, jak się dalej okaże mają fundamentalne znaczenie w koncepcji ewolucji Wszechświata. Czterowyrazowy termin jest kłopotliwy i może być powodem nieporozumień semantycznych. Szczęśliwie się składa, że w wartość liczbową intropii, oprócz oddziaływań termodynamicznych i wynikających z obecności informacji („oddziaływań informacyjnych”) wchodzą także inne oddziaływania fizyczne, rozpoznane w kosmologii. Te oddziaływania są charakteryzowane przez „stałe sprzężenia” oznaczane literą grecką alfa z indeksem literowym. Np. stała sprzężenia oddziaływań jądrowych silnych przez α_s(strong), stała sprzężenia oddziaływań słabych przez α_w (weak), grawitacyjnych przez α_g,elektromagnetycznych przez α_elmg. W notacji „kosmicznej” te stałe oddziaływań są wykładnikami potęg liczby Φ. Idźmy tym tropem i nazwijmy wykładnik A stałą sprzężenia oddziaływań termodynamicznych, a wykładnik B stałą sprzężenia oddziaływań informacyjnych. Odpowiednie wartości intropii wyniosą: I_td=Φ^A oraz I_inf=Φ^B. Ale intropia uwzględniająca oba te oddziaływania, zgodnie z wzorem (8-1), będzie: I=(Φ^A)^B czyli I=Φ^AxB.

Niech stała A będzie liczbą ujemną (bo dotyczy ciągle rosnących strat), a stała B dodatnią (bo dzięki obecności informacji powoduje zmniejszenie tempa wzrostu strat).

Na podstawie tego, co napisałem w poprzednim podrozdziale, możemy sformułować równania:

AxB=-166,476 3383, oraz

B=A + (3+Φ^-2)

Mamy układ dwóch równań z dwoma niewiadomymi, a więc z łatwością mogą być doprowadzone do postaci równania kwadratowego. Rozwiązaniami tego równania są:

A=11, 321 9245

B=A +3+Φ^-2 = 14,703 890 52

Sprawdźmy: -11, 321 9245 x 14,703 89052 =-166,476 3383.

Mamy oto stałe oddziaływań termodynamicznych i informacyjnych, charakteryzujące kompletny wielowszechświat, a pośrednio każdy cykl ewolucji tego wielowszechświata.

Wróćmy do długości Plancka. Jeżeli to ma być w naszej fazie ewolucji najmniejsza sensowna długość odcinka (oznaczę ją przez „jP”), to (jP)² jest najmniejszą sensowną powierzchnią, a (jP)³ najmniejszą sensowną objętością. Według kosmicznego systemu liczbowego wszystkie trajektorie, na których odbywają się zmiany stanów kwantowych materii, są spiralami logarytmicznymi, na ogół tzw. spiralami logarytmicznymi „złotymi”, a niekiedy „srebrnymi”.

W spirali złotej każdorazowa zmiana stanu o krotność Φ jest związana z obrotem promienia wodzącego spirali o 90 stopni, czyli π/2 radianów. W spirali srebrnej zmianie stanu o krotność Φ towarzyszy obrót promienia o 180 stopni, czyli π radianów.

Przypuśćmy, że przy obrocie promienia wodzącego trajektorii spiralnej o 90 stopni zmiana stanu polega na Φ-krotnym zmniejszeniu masy (a więc energii potencjalnej) cząstki lub układu cząstek.

Tej zmianie towarzyszy oczywiście zmniejszenie objętości przestrzeni, zajmowanej przez grudki materii w stopniu Φ³-krotnym, to z kolei oznacza spadek gęstości masy/energii materii w tej przestrzeni w stopniu Φ²-krotnym. Gęstość masy/energii wydaje się dostatecznie bliska gęstości prawdopodobieństwa znalezienia cząstki we wnętrzu arbitralnie wybranej bryły geometrycznej, a więc, jak sądzę, można tę wielkość fizyczną uznać za adekwatną z intropią grudek materii w punktach trajektorii określonych przez kąty obrotu promienia, np. co 90 stopni. Takie „rozumowanie”, jeżeli zrezygnować z daleko posuniętej ścisłości matematycznej, wydaje się bliskie zarówno prawom fizyki klasycznej, jak i kwantowej, a tym samym atrakcyjne z punktu widzenia dydaktycznego. Prezentacja graficzna jest sprawdzonym w prezentacjach pisanych i ustnych środkiem ułatwiającym animację wyobraźni czytelników albo słuchaczy. W tej opowieści jest to sprawa o dużym znaczeniu.

1.8.3 Intropia. Różnica między intropią termodynamiczną i informacyjną.

Musimy wrócić do rozdziału 1.8.1 i dla uniknięcia nieporozumień poświęcić więcej miejsca intropii informacyjnej, będącej prawdopodobnie nowością terminologiczną. Znane są kłopoty ze zrozumiałym, a jednocześnie z poprawnym, zdefiniowaniem entropii. Już na wstępie rozdziału 8 przestrzegałem przed utożsamianiem entropii z intropią, pojęciem stworzonym na użytek tej opowieści. A jednak oba te pojęcia mają coś wspólnego, bo wynikają z odwiecznego szukania odpowiedzi na pytanie: jaki jest kres wszelkich rzeczy skoro już w niezupełnie jasny sposób powstały i trwają? Odpowiedzi kreacjonistyczne umykają z domeny nauki, są bowiem źródłem jeszcze większych wątpliwości.

Wprowadzając pojęcie intropii informacyjnej wkraczamy także na niepewny grunt. Pierwszym stwierdzeniem mogłoby być takie, że intropia termodynamiczna jest potrzebna do odpowiedzi na pytanie o los materii, natomiast intropia informacyjna dotyczy losów informacji, jaka rodzi się i towarzyszy każdemu krokowi zmiany stanu każdej cząstki tej materii. Dlaczego w pracach Susskinda, Hawkinga i innych wybitnych fizyków problem informacji pojawił się publicznie tak późno, w pierwszej dekadzie XXI wieku? Tu akurat odpowiedź jest łatwa. Informacja, jeżeli w ogóle ją dostrzegano poza informatyką, była traktowana jako coś tak samo oczywistego, jak materia, w tym sensie, że jeśli cząstka materii ulegała rozpadowi, to podobnemu rozpadowi i unicestwieniu podlegała informacja. Gdy zdarzyło się, że materia wpadła do czarnej dziury, to towarzysząca jej w niezdefiniowanej postaci informacja ginęła wraz nią i „nie było sprawy”. Wszystko wydawało się stosunkowo proste. Dopiero Leonard Susskind i wybitny noblista holenderski Gerard t”Hooft wystąpili otwarcie z negacją takiego poglądu, mając po przeciwnej stronie większość fizyków z Hawkingiem na czele. Wiadomo, jak skończyła się ta walka poglądów, choćby z wspomnianej już książki Susskinda „Bitwa o czarne dziury”. A więc grunt, na który wstępujemy nie jest aż tak grząski; prawo zachowania energii jest we współczesnej nauce prawem zachowania energii i informacji. Skoro tak, to pytania o przeszłość i przyszłość informacji są w pełni zasadne.

Intropia termodynamiczna I_td w równaniu (8-1), podrozdziale 8.1, określa wielkość strat masy i energii potencjalnej w trakcie ewolucji Wszechświata. Nie ma tu pojęcia zysku masy lub energii, każda nowa faza ewolucji, albo inaczej każda zmiana stanu kwantowego Wszechświata o skończonych rozmiarach wiąże się z ubytkiem tych wielkości, albo w nielicznych przypadkach z ich niezmiennością. W odróżnieniu od entropii nie piszemy tu o rosnącym „nieuporządkowaniu” materii w rozpatrywanej zamkniętej przestrzeni, którą w wielu publikacjach popularnonaukowych nazywa się kolokwialnie, ale zrozumiale, pudłem. Terminy „porządek” i „bałagan” są nazbyt subiektywne, co z pewnością jest dobrze znane fizykom teoretykom patrzącym na swoje biurka.

To „nieuporządkowanie” albo przeciwnie: ukryta dążność natury do porządku (tak!) wyrazimy za pomocą pojęcia intropii informacyjnej. W dużym skrócie: z intropią termodynamiczną mamy do czynienia w każdej fazie ewolucji Wszechświata, ponieważ w każdej fazie podlega on procesom termicznym. Intropia informacyjna daje się doświadczalnie zaobserwować tylko w pewnych fazach ewolucji, a mianowicie tuż przed przekroczeniem przez materię, której ta informacja dotyczy, horyzontu kosmologicznego, niezależnie od tego, jak ten horyzont nazwiemy. Ta informacja, choć pozbawiona wspomnianej materii, nie ulega jednak zniweczeniu, bo jest to niemożliwe tak samo, jak nie jest możliwe zniweczenie energii. Zostaje ona zarejestrowana w postaci kwantów pola Psi (Ψ) w pamięciach hierarchicznie większych obiektów, albo, w razie ich wypełnienia, w nieograniczonych zasobach pamięci nadprzestrzeni, skąd na zasadzie losowej mogą znaleźć się w nowo tworzonych wszechświatach, trochę podobnie do dziedziczenia genów w biologii.

1.8.4 Intropia (IV). Oddziaływania fizyczne określające wartość intropii Wszechświata.

Fakt kolejnego powrotu do problematyki intropii świadczy, że to pojęcie powołane jako zamierzone wsparcie przedstawianej tu koncepcji kosmologicznej, a więc dotąd raczej niespotykane, jest wieloznaczne i, co tu ukrywać, trochę mętne. Zapewne świadczy to także o tym, że ta „mglistość” pojęcia jest także dostrzegana przez autora.

W podrozdziale 8.2 usiłowałem przekonać czytelnika, że w odróżnieniu od entropii, mającej swoje dobrze utrwalone miejsce w nauce, intropia uwzględnia istnienie innych znanych i zmierzonych oddziaływań fizycznych. Decyzja, żeby później porównać uzyskane tą drogą wyniki z punktem widzenia Rogera Penrose wynika z niewątpliwego podziwu i zaufania do tego Uczonego, ale nie tylko. Ktoś, kto interesuje się problematyką entropii w szerokim znaczeniu, a więc problematyką przemijania, rozpadu, łatwości tworzenia bałaganu i trudności z utrzymaniem względnego porządku, wreszcie kresu egzystencji, a zatem również sensu tej mijającej egzystencji, z całą pewnością z irytacją zauważy, że z rozmaitych źródeł nie otrzymuje jednoznacznej odpowiedzi na nurtujące pytania bądź wątpliwości. W takiej sytuacji pozostaje zwrócić się do obdarzonych zaufaniem autorytetów. Stephen Hawking, znany nie tylko jako wielki uczony i myśliciel, ale także jako humorysta, „wyjaśnił” swoim słuchaczom:

Jeśli po każdym praniu znajdujecie jedną skarpetkę nie do pary, to znaczy, że macie do czynienia z entropią Natury.

Zabawne, ale, co tu ukrywać, bardzo celne stwierdzenie. Jeszcze raz potwierdza się, że tylko prawdziwi, nie udawani znawcy złożonego problemu, są w stanie przedstawić jego sedno w sposób zrozumiały. Proszę zatem o wyrozumiałość w kwestii intropii i nie tylko.

O jakich oddziaływaniach będziemy tu opowiadać? Lista jest (na razie?) niewielka:

*) oddziaływania termiczne i termodynamiczne,

**) oddziaływania elektromagnetyczne,

***) oddziaływania grawitacyjne,

****) oddziaływania jądrowe silne,

*****) oddziaływania jądrowe słabe.

Nie cieszmy się, że jest ich tylko pięć. Mamy podstawy, żeby przypuszczać, że w miarę postępów nauki i eksperymentów, badacze będą odkrywać nowe zależności w „organizmie” Wszechświata. W świetle tego, co zostało wzmiankowane w rozdziale 1 i co zostanie opisane dalej w aspekcie struktury opisywanego w tej książce Wszechświata, wydaje się konieczne uwzględnienie w intropii jeszcze innych oddziaływań, których obecności nie stwierdzono w obowiązującym w nauce Modelu Kosmologicznym. Do takich należą: oddziaływania informacyjne, jako skutki istnienia i obiegu informacji oraz oddziaływania będące skutkiem istnienia sił skrętnych (proszę nie mylić z siłami powodującymi rotację obiektów kosmicznych). Te ostatnie nazwę oddziaływaniami skrętnymi i będą wymiarowane stałą sprzężenia oddziaływań skrętnych.

W kwestii tych ostatnich przypomnijmy, że znamy podobne zjawisko z codziennego życia w postaci wirującego strumienia wody wypływającej z wanny albo umywalki, o coraz mniejszym promieniu wiru i coraz większej prędkości obwodowej. Jest to zjawisko z zakresu hydrodynamiki. Znane są także inne obserwacje potwierdzające, że mamy do czynienia z przejawem znanych w Kosmosie i na Ziemi praw fizyki, np. zjawisko wiru akrecyjnego, należące do domeny astrofizyki. Ale bywają również inne, znane z życia domowego efekty skręcania się strumienia materii, o odpowiednio dobranych własnościach, takich jak lepkość. Proszę przypatrzeć się uważnie cienkiemu, pionowemu strumieniowi miodu przelewanego z jednego naczynia do drugiego. Powstający na dole strumienia stożek wiru nie został, jak się wydaje, wyjaśniony dotychczas przez naukę, co potwierdzili autorzy interesującej publikacji pt. Sztuczki z ciekłą liną w „Świecie Nauki” (marzec, 2014) Neil M. Ribe, Mchali Habibi i Daniel Bonn z różnych ośrodków naukowych we Francji, Holandii i Iranie. Jak widać, nawet przed fizyką procesów kuchennych jest jeszcze wiele do zrobienia.

Wróćmy do oddziaływań. W zapisie „zrozumiałym dla Kosmosu” intropia wywołana przez każde z wymienionych oddziaływań będzie miała postać matematyczną Φ^(SS⁾, gdzie pod skrótem (SS) kryje się „stała sprzężenia” charakterystyczna dla każdego z oddziaływań i określająca jego siłę. Niektórzy autorzy oznaczają stałe sprzężenia grecką literą alfa z odpowiednim indeksem w lewym dolnym rogu:

α^-1 bez indeksu dolnego zarezerwowana jest dla odwrotności stałej struktury subtelnej, ale w celu podkreślenia, że dotyczy sprzężenia elektromagnetycznego, intropię elektromagnetyczną będziemy zapisywać, jako:

Φ_elmg = Φ^1/α,

α_s oznacza stałą sprzężenia dla oddziaływań jądrowych silnych (strong),

α_woznacza stałą sprzężenia dla oddziaływań jądrowych słabych (weak),

α_grav oznacza stałą sprzężenia dla oddziaływań grawitacyjnych.

Oddziaływania termodynamiczne i informacyjne już połączyliśmy jednym związkiem matematycznym (wzór 8-1):

z taką poprawką jednak, że symbol I_całkbędzie odnosił się dalej do intropii całkowitej, obliczonej z uwzględnieniem wszystkich innych oddziaływań, jeśli będzie to możliwe za względu na znajomość danych. Intropię infotermodynamiczną oznaczymy skrótem

α_toznacza stałą sprzężenia dla oddziaływań skrętnych (twist).

Intropia całkowita układu zamkniętego, a Wszechświat za taki uważamy w tej opowieści, wyniesie (wzór nr 8-2):

I_całk= Φ^infotdx Φ^elmgx Φ^gravx Φ^strongx Φ^weakx Φ^twist

O ile dla oddziaływań jądrowych istnieją wyniki teorii i doświadczeń, dając przynajmniej pojęcie o zgrubnej wartości liczbowej, o tyle z pozostałymi składnikami intropii całkowitej Wszechświata będą poważne kłopoty. Do sensownej oceny będą bowiem niezbędne wyjaśnienia struktury Wszechświata, do której (i zapewne wyłącznie do niej) odnoszą się robione szacunki. Dobitnym przykładem mogą być oddziaływania grawitacyjne, dla których rolę stałej sprzężenia odgrywa niezbyt przekonująco stała grawitacji G, natomiast same oddziaływania w przyjętym Modelu są najsłabszymi spośród pozostałych, średnio 10⁴⁰ razy mniejszymi. W przedstawianym w tej książce modelu Wszechświata, będącego efektem wybuchu nie jednej pragwiazdy (czyli tzw. Big Bang’u), ale trzech współuwikłanych gwiazd w stanie tzw. pragmatropii kwantowej, oddziaływania grawitacyjne awansują, obok elektromagnetycznych, do naczelnych, decydujących o strukturze i ewolucji Wszechświata.

Z tego powodu przerwiemy w tym miejscu opis intropii, żeby do dalszego jego ciągu powrócić na zakończenie Części IV-tej i jeszcze w V-tej, kiedy znana będzie czytelnikowi struktura Wszechświata według wyobrażeń autora oraz kiedy okaże się, czy jest możliwe sensowne ilościowe oszacowanie wartości stałych sprzężenia.

1.9 O pewnym oddziaływaniu grawitacyjnym, odpowiedzialnym za ekspansję Wszechświata.

1.9.1 Traktrysa i jej asymptota.

Na zakończenie I-ej części tej opowieści przyszła pora na przedstawienie propozycji, której nowość, a więc także znaczne ryzyko kompletnego nieporozumienia, przez kilka lat bardzo mnie onieśmielały. Chodzi o przyczynę tych okresów ewolucji, w których Wszechświat mniej lub bardziej gwałtownie się rozszerza, podobnie jak nadmuchiwany balon, jeśli użyć zdecydowanie nadużywanego w literaturze kosmologicznej porównania.

Przypomnę aktualne ustalenia nauki.

Pierwszy okres ekspansji, zwany „inflacją”, zdarzył się ok. 10^-36 sekundy po domniemywanym Wielkim Wybuchu (czas „zero”) i trwał ok. 10^-32 sekundy, w którym to przedziale czasu Wszechświat powiększył objętość o czynnik co najmniej 10⁷⁸. A wszystko to odbyło się za sprawą „pola inflatonowego”, o którym poza nazwą, właściwie nic pewnego nie wiadomo. Inflacja skutkuje do dzisiaj wielką (zdaniem naukowców) jednorodnością i izotropią Wszechświata.

Po zakończeniu ery inflacji nastał czas spokojnej ekspansji Wszechświata, który trwa i będzie trwał do nieprzewidywalnego końca jego dziejów. Za rozszerzanie się Wszechświata tym razem odpowiedzialna jest tzw. „ciemna energia”, o której wiadomo, że stanowi ok. 70% energetycznej zawartości Wszechświata. Po zakończeniu pierwszego etapu misji satelity Planck, ESA uściśliła dane z wartości 72,8% na 68,3%.

Podobne uściślenie danych dotyczyło tzw. „ciemnej materii”, skutkującej m.in. ”nadmiernie” szybką rotacją kulistych gromad galaktyk: z 22,7% na 26,5% zawartości. Tak więc wydaje się, że nauka zdobyła sporą wiedzę o własnościach obu „ciemnych” składników Wszechświata, niestety poza jedną: nadal, jak się wydaje, nie wiemy, co to właściwie jest i skąd czerpie takie zasoby energii. Te dane, przedstawione przez ESA publicznie w dniu 21 marca 2013 r. potwierdzają wcześniejsze przewidywania, że znana nam materia i promieniowanie zajmują zaledwie od 4,5 do 4,9% energetycznej zawartości Wszechświata.

To, co wyżej napisałem, mniej lub bardziej adekwatnie do aktualnych konstatacji nauki, nie nadaje się do wykorzystania w niniejszej opowieści, mogłoby bowiem powodować zacieranie się różnicy między wiedzą naukową a fantazjowaniem rozlicznych pseudonaukowców. Historia dociekań teoretycznych i eksperymentalnych w przypadku ciemnej materii liczy sobie już ok. 35 lat. Na totalną klęskę wygląda fakt, że w sierpniowym (2018) numerze „Scientific American” („Świat Nauki”, nr 9, 2018) ukazał się artykuł pod zaskakującym tytułem: Is Dark Matter Real?, „Czy ciemna materia istnieje?”. Po 3,5 dekadach! Autorzy stwierdzają tam m.in. „…zmiana równań grawitacji nadal wydaje się sensowną drogą postępowania”. Doceniam „odkrywczą” śmiałość autorów.

A zatem, jaka to energia, powodująca każdą możliwą ekspansję Wszechświata i gdzie jest jej źródło?

Będzie wyglądało na żart w nienajlepszym gatunku, jeśli napiszę, że odpowiedź jest nam udzielona tu, na Ziemi, w przenośni i w realu. Bo na ziemi, zwłaszcza zaśnieżonej, albo na piasku, właściciele piesków, na ogół niesfornych, zauważyli podczas codziennych spacerów z ich ulubieńcami, że pieski prowadzone na smyczach o stałej długości (ważne!) chciałyby oddalić się od swoich opiekunów i powodują, że smycz jest stale lekko naprężona. Wyobraźmy sobie, że w miejscu startu napięta smycz jest prostopadła do prostoliniowej ścieżki. Ale właściciele mają swoje obowiązki i starają się wymusić na pieskach powrót na prostą ścieżkę, którą zamierzają dalej spokojnie iść. I właśnie wtedy zauważyli, że ślady pozostawione przez psie łapy, na śniegu albo na piasku, tworzą krzywe nieznane z lekcji geometrii w szkole, ba, nawet ze studiów, które są do siebie podobne (pieski, jak zaznaczyłem są trochę niesforne), a poza tym te krzywe są po prostu ładne.

Są jeszcze inne anegdoty o genezie takich krzywych, które nazwano dużo później traktrysami. Ta nazwa to już naprawdę nie mój wymysł, poszukiwania autora tej nazwy sięgają Leibniza i Huygensa, co jest możliwe z tego względu, że jej źródłem jest język łaciński (tracto – ciągnę). Traktrysa, zaliczana do tzw. krzywych ciągnionych, nie istnieje sama sobie, ma swoją asymptotę, prostą, do której leżące na krzywej punkty nieustannie się zbliżają. W podanej wyżej anegdocie asymptotą jest prosta ścieżka, którą podąża lub usiłuje podążać właściciel pieska. Analiza matematyczna wykazała, że długość tej ścieżki niezbędna do tego, aby piesek znalazł się w końcu na ścieżce, w odległości równej długości smyczy od właściciela (nazwijmy tę długość promieniem traktrysy i znaczmy ją dużą literą R) jest nieskończenie wielka jest nieskończenie wielka. Trzeba więc przestrzec właścicieli piesków, że ich pieski nigdy nie znajdą się na ścieżce (o ile ci właściciele nie odważą się użyć środków przymusu bezpośredniego) i to wcale nie jest ich wina, tak po prostu zadecydowała Przyroda.

No dobrze, niech tak będzie, ale jaka to „Przyroda”?

Odpowiedzi udzielili matematycy, którzy wzięli traktrysę pod lupę. Okazało się, że najbardziej zaskakującą cechą tej krzywej jest to, że do jej analitycznego wyznaczenia trzeba sięgnąć po funkcje trygonometrii hiperbolicznej, ponieważ krzywizna tej figury w każdym jej punkcie jest ujemna. A więc nie tylko przekrój powierzchni siodła końskiego może mieć taką właściwość.

Teraz już wiemy, co to za „Przyroda” nakazała pieskom trzymać się z dala od ścieżki, którą chce iść na spacer ich pan, albo częściej pani. Proszę jeszcze raz przeczytać rozdział 5 tej opowieści p.t. Geometrie Przestrzeni. To alternatywna, niedostępna dla nas przestrzeń „ujemna” uśmiechnęła się do nas, Ziemian, by dać nam jakąś wskazówkę. Nie zmarnujmy tej okazji.

Czas więc, żeby przedstawić bohaterów tego rozdziału.

Traktrysa i jej asymptota są figurami geometrycznymi na wspólnej płaszczyźnie, na której asymptota jest obiektem jednowymiarowym, a traktrysa dwuwymiarowym.

Najważniejszą cechą tego układu, którą później będę nazywać „prawem traktrysy” jest to, że styczne do krzywej w dowolnym jej punkcie, mające niezmienną długość, zwaną promieniem traktrysy, łączą te punkty z przeciwległymi punktami leżącymi na asymptocie. Powracając do anegdotki z pieskami, oznacza to, że smycz, której koniec trzyma ich właściciel, w ciągu spaceru ma stałą długość. Wyjaśnię to na ilustracji 9-1.

Ilustracja 9-1. Traktrysa matematyczna (pomarańczowa) z naniesionymi na nią punktami (czerwonymi) o współrzędnych zgodnych z zapisem kosmologicznym (patrz tekst). Pokazano przykładowo dwie styczne o niezmiennej długości, równej promieniowi traktrysy.

Krzywa w kolorze pomarańczowym jest traktrysą, a oś X (niebieska) jej asymptotą. Dla przykładu pokazano tylko dwie styczne (czarne) w zakresie zmiennej x od zera do trzech. Promień traktrysy matematycznej, czyli takiej, której przebieg uzyskano na drodze obliczeń na podstawie znanych równań, ma wymiar 1 (w skali, jaką przyjąłem w swoim komputerze wynosi on 100). Jak już wspomniałem równania te zawierają funkcje hiperboliczne i obliczenia bez odpowiednich narzędzi programowych są dość kłopotliwe, a przede wszystkim (jeżeli się to robi po raz pierwszy) bardzo czasochłonne. Nie mogę sobie pozwolić na „ręczne” obliczenia, wymagające wcześniej zdobytej, niezwiązanej bezpośrednio z zasadniczym tematem, wiedzy i sporo czasu. Z tego względu skorzystałem z gotowych obrazów zamieszczonych na godnych zaufania portalach i stronach publikacji matematycznych, przenosząc odczytane wartości współrzędnych X i Y, punkt po punkcie, na ekran komputera. Dokładność odwzorowania jest więc zależna od dokładności obrazu źródłowego i dokładności z jaką odczytywałem wartości współrzędnych. Zrobiłem to dla kilku odrębnych źródeł i na tej podstawie twierdzę, że czerwona krzywa na ilustracji 9-1 odpowiada traktrysie matematycznej z dokładnością nie gorszą niż 1% i dlatego dalej będę tak uzyskane traktrysy nazywać, trochę na wyrost, matematycznymi.

Patrząc na ilustrację, staje się uzasadnione moje zainteresowanie rozważanym układem tych dwóch figur. Jeżeli wprowadzić do rozumowania klasyczny czas, czyli uznać, że właściciel pieska jednak posuwa się do przodu (np. z punktu o współrzędnych (0, 0) do punktu o współrzędnych (0, 2), to w tym czasie hipotetyczny piesek odbywa na krzywej (bo musi pod wpływem działających na niego sił) inną podróż (z punktu (0, 1) do punktu (0, 0,284) ). Nieprzymuszony siłą piesek nigdy nie znajdzie się za swoim panem na ścieżce, chyba że w nieskończoności, ale w tej Opowieści nie ma miejsca na takie pojęcie.

Dane na osiach współrzędnych według systemu dziesiętnego mogą być „przetłumaczone” na system liczbowy kosmiczny, według następującego „kodu”, wynikającego z wyjątkowych własności kosmologicznej cyfry Φ:

Jak widać, traktrysa kosmologiczna daje się wyrazić analitycznie z użyciem tylko jedynki i liczby Φ. Jest to jakaś wskazówka, niestety nie dowód, że poszukiwania związku traktrysy z Kosmosem nie są zupełnie bezpodstawne.

W tej transformacji istnieją pewne zastanawiające prawidłowości:

*) Można wyróżnić dwa rodzaje transformacji: według zasady (Φ^-n) na górze słupka, oraz według zasady (Φ^-Φx Φ^-n), dla czterech dolnych wersów.

**) Uciekająca od powyższej zasady rzędna 0,532… jest średnią geometryczną wartości sąsiadujących 0,618… i 0,459… sprawiając wrażenie, że jest łącznikiem dwóch zasad transformacji.

***) Rzędne o wyżej podanych wartościach, odpowiadające tym punktom na osi X, które wyrażają się według zasady (Φ^-n), nieco odbiegają od wartości tych samych rzędnych dla traktrysy matematycznej. Odchyłki są poniżej 0,5%, największa dla rzędnej 0,532. Zastanawiające jest wszakże to, że odchyłki dodatnie występują naprzemiennie z odchyłkami ujemnymi, co sugeruje, że to może nie być przypadkowe i w jakiś sposób jest wliczone w prawo traktrysy. Pokazano to na ilustracji 9-2.

Ilustracja 9-2. Traktrysa kosmologiczna

Krzywa pomarańczowa: traktrysa matematyczna. Czerwone punkty na krzywej ciągłej pokazują wartości rzędnych w systemie liczbowym Wszechświata (patrz tekst) Pogrubiona czarna linia schodkowa: aproksymacja traktrysy kosmologicznej dla 6 poziomów intropii wyznaczonych przez rzędne „kosmologiczne”. Poziomy y=od 1 do 0,618 pominięto, ponieważ w tym zakresie rzędnych i odciętych (x=0 – Φ^-3) pochodna traktrysy musi przyjąć wartość zero przez co ta część traktrysy nie ma oczywistego przełożenia kosmologicznego. Cienkie ukośne linie czarne są przykładowymi stycznymi o długości ok. 1. (patrz ilustracja 9-1).

Dla pełniejszej wiedzy o rozpatrywanym tu układzie trzeba wspomnieć o pewnej subtelności przebiegu traktrysy w otoczeniu punktu o współrzędnych (0, 1). Otóż z analizy matematycznej tej krzywej wynika, że przy starcie pochodna krzywej w punkcie (0, 1) przyjmuje wartość zero, co wynika z przyjętego wcześniej założenia, że na starcie smycz pieska jest prostopadła do ścieżki spacerowej jego opiekuna. Autorzy jakby o tym zapominają i rysują przebieg traktrysy tak, jakby opiekun zaczynał swój ruch od x=0,236, czyli(Φ^-3). (Patrz. Ilustracja 9-1). Prawda jest taka, że przy zmianie x od zera do Φ^-3zmiana położenia adekwatnego punktu na krzywej jest niezauważalna, a piesek nie odczuwa jeszcze działania pociągającej go siły, jego prędkość pozostaje bliska zeru.

To jednak nie wszystko, co się wiąże z upływem klasycznego czasu. Twierdzę, że układ traktrysa asymptota jest układem odwracalnym co do kierunku ruchu na asymptocie. Właściciel pieska po osiągnięciu punktu (0, 2) może zmienić kierunek swojego ruchu na odwrotny i zjawisko wykreślania przez pieska trajektorii swojego ruchu powtórzy się à rebours, od punktu (0, 0,284) do punktu (0, 1). Nie sugerujmy się giętkością smyczy, może to być hipotetyczny sztywny hol. Zamiast „wleczenia” będziemy mieli do czynienia z pchaniem. W obu postaciach tego samego zjawiska muszą działać takie same siły (np. odpychanie punktu na krzywej od asymptoty), a także musi brakować tych samych sił klasycznej natury: tarcia, grawitacji, i być może innych, które by zakłóciły zakładane z góry idealizowane warunki.

Punkty na asymptocie i na krzywej nie poruszają się z taką samą prędkością. Choć startują z końców ukośnej stycznej, łączącej punkt x=1, y=0,284 z punktem x=2, y=0,108 (patrz ilustracja 9-1), to „metę” na osi y, ( x=0) osiągają jednocześnie. Rozpatrujemy szybkości dużo mniejsze od szybkości światła, więc pojęcie „jednoczesności” ma tu znaczenie klasyczne. Najistotniejsze jest to, że odległość obu sprzężonych ze sobą punktów cały czas pozostaje niezmienna (w języku nauki byłaby niezmiennicza), równa promieniowi traktrysy, przyjętemu z definicji jako klasyczna jedność.

1.9.2 Traktrysa kosmologiczna.

Jakie to wszystko, co napisałem wyżej, może mieć znaczenie w prezentowanej tu „opowieści o kosmologii”? Powróćmy na chwilę do rozdziału 6.3. W warunkach wyidealizowanego tzn. idealnie ortogonalnego i symetrycznego Wszechświata dwie cząstki materii o takich samych masach, ale o przeciwnych znakach ładunków grawitacyjnych (grawionów) pozostają w nierozerwalnym „uścisku”, podobnie jak dwaj zapaśnicy o takich samych możliwościach fizycznych i mentalnych, albo jak dwaj zawodnicy mocujący się „na ręce”, których ramiona przed zbliżającym się rozstrzygnięciem zaczynają drżeć. Albo jak niewolnik Ursus w walce z potężnym turem na rzymskiej arenie cesarza Nerona w powieści Henryka Sienkiewicza Quo Vadis? Krótki cytat będzie tu poglądowym przerywnikiem w tym tekście:

…I człowiek, i zwierz trwali w takiej nieruchomości, iż patrzącym zdawało się, że widzą jakiś obraz przedstawiający czyny Herkulesa lub Tezeusza lub grupę wykutą z kamienia. Ale w tym pozornym spokoju znać było straszliwe natężenie dwóch zmagających się ze sobą sił.

Analogie te nie są bardzo oderwane od interesującego nas zjawiska kosmologicznego z udziałem traktrysy. Wspólną cechą jest bowiem to, że w trakcie „zapasów” w przestrzeni między zmagającymi się mocarzami, którą możemy sobie wyobrazić, jako szczelinę między lokalną przestrzenią dodatnią, a lokalną przestrzenią ujemną, gromadzi się olbrzymia energia potencjalna, która w końcu musi skutkować jej wyzwoleniem gdy przekroczona zostanie jakaś wartość krytyczna.

„Szczeliny”, o których napisałem akapit wyżej są ważne dla całej tej opowieści. W tu opisanej, czyli najogólniejszej formie, szczeliny będę nazywał „szczelinami A” od słowa Antygrawitacja, podkreślając, że warunkiem ich powstawania jest współobecność materii o grawitacji ujemnej.

Drżenie ramion zapaśników „na ręce” są objawem pojawiającej się energii kinetycznej i zapowiedzią takiego właśnie rozstrzygnięcia. Tylko w jednym wypadku to nie nastąpi: wtedy, gdy obie zmagające się strony otrzymują „z boku” podtrzymującą ich siły energię w takich samych porcjach. Ale i to jest tylko „pół prawdy”, ktoś albo coś musi tę dodatkową energię dostarczać, a więc i nią „płacić” ze swoich zasobów energetycznych. Nie może być inaczej. I to jest właśnie ta okoliczność, która zdecydowała, że prawo traktrysy znalazło się w polu moich zainteresowań kosmologicznych. Tak doszło do wyodrębnienia pojęcia traktrysy ”kosmologicznej” oraz trójwymiarowego modelu całego układu. Zdaję sobie sprawę z tego, że nadużywam w tekście przymiotnika „kosmologiczny”, kiedy nie mam jeszcze pewności, że jest on wcześniej przekonująco uzasadniony. Proszę o wyrozumiałość.

Jak już napisałem traktrysa matematyczna jest tworem dwuwymiarowym, a jej asymptota jednowymiarowym. Na takie byty nie ma miejsca we Wszechświecie według prezentowanej tu hipotezy. Nie ma tu miejsca ani na płaszczyznę ani na prostą, ani na nieskończoność, ani na „osobliwość”. Wszystko jest zakrzywione wskutek działań grawitacyjnych, elektromagnetycznych i innych oddziaływań rozpoznanych i opisanych przez naukowców. Wszystko też ma swoje granice. Wyjątkiem wydaje się być nadprzestrzeń, ale, jak już pisałem, jest ona na granicy moich rozważań i wyobraźni.

Kosmologiczne aspekty prawa traktrysy są zbyt pociągające, żeby z nich rezygnować. Postanowiłem sprawdzić, czy traktrysa i jej asymptota dadzą się wyrazić za pomocą kosmicznego systemu liczbowego (por. rozdz. 2), a także, czy jest możliwa trójwymiarowa postać graficzna układu z zachowaniem prawa traktrysy. Wszechświat, nawet „ten mój”, jest bytem co najmniej trójwymiarowym, a według różnych teorii naukowych może być nawet dziewięcio- lub jedenastowymiarowym. Na razie moje wymagania w tej kwestii pozostają bardzo skromne, wystarczą trzy wymiary. Wyniki moich usiłowań w pierwszej z wymienionych kwestii są pokazane na Ilustracjach 9-1, 9-2 A i B i częściowo wyjaśnione w tekście pod nimi.

Można się zastanawiać nad tym, czy wartości rzędnych traktrysy kosmologicznej między zaznaczonymi niebieskimi kółeczkami na rysunku B wynikają z monotoniczności krzywej i przyjmują wtedy wartości pośrednie, czy też zachowują się „dwustanowo”, jak to pokazuje czerwona linia schodkowa. Jeśli chodzi o pierwszą możliwość nie mam argumentów przemawiających za jej słusznością. Należy bowiem przypomnieć, że we Wszechświecie kwantowym nie ma płynności zachowań, ruchu, szybkości, przyśpieszenia i innych zjawisk, jakie postrzegamy naszymi zmysłami i przyrządami w świecie klasycznym. Wszystko jest stawaniem się, nieustannymi wibracjami i kwestią prawdopodobieństwa. Nie można wykluczyć, że prawa traktrysy zastosowane w Kosmosie również podlegają tej zasadzie i wtedy schodkowa aproksymacja traktrysy kosmologicznej ma sens. W jaki sposób można to sprawdzić? Moim zdaniem skokowe zmiany wartości rzędnych traktrysy muszą się ujawnić w obliczeniach intropii Wszechświata. Powrócę do tej kwestii w Części III.

Nie znam oczywiście uzasadnienia dla takich „prawidłowości”. Uznaję, że prawa jak najdłuższego przetrwania Wszechświata i minimalizacji wydatków „przydzielonej” mu energii tego widocznie wymagają.

1.9.3 Traktrysa kosmologiczna i jej asymptota w przestrzeni trójwymiarowej.

„Prawo traktrysy” zostało sformułowane dla krzywej na płaszczyźnie, przestrzeni dwuwymiarowej. Jeżeli ma ono mieć zastosowanie w kosmologii musi zostać przetransformowane dla przestrzeni trójwymiarowej. Obserwowalny Wszechświat jest tworem co najmniej trójwymiarowym, są bowiem naukowe teorie kosmologiczne, np. teorie strun w kilku wariantach, według których Wszechświat jest bytem dziewięcio-, a nawet jedenastowymiarowym. Z braku dostatecznych narzędzi programowych, a także niedostatecznych umiejętności, podjąłem się wykonania tego zadania według zasady: „tnij i przymierzaj” (ang. cut and try) z dużym udziałem własnej intuicji. Z zażenowaniem przyznaję, że zabrało mi to około dwóch lat pracy nad tekstem tej opowieści, po czym okazało się, że sprawa jest dużo łatwiejsza, niż początkowo zakładałem. Może nie będzie to jednak zaskakujące, gdy wziąć pod uwagę, że oprócz „prawa traktrysy dwuwymiarowej”, o której napisałem w rozdziale 9.1, „prawo traktrysy trójwymiarowej’ (w skrócie traktrysy 3D) musi uwzględnić dodatkowo następujące warunki:

– asymptota z obiektu jednowymiarowego musi się stać trójwymiarowa, co oznacza poważną zmianę konstrukcji całego układu, znanego z ilustracji 9-1,

– pojęcie „stycznej” do traktrysy, która otrzymała grubość, w dodatku nietypową w geometrii klasycznej, staje się bardzo niejednoznaczne; wystarczy wyobrazić sobie „styczną” do kuli (stycznych będzie wtedy nieskończenie wiele), dlatego w przypadku traktrysy 3D zamiast stycznych będziemy mieli do czynienia z „normalnymi”, tworzącymi w punktach przecięcia z krzywą i jej asymptotą kąty proste,

– promień R, który na płaszczyźnie był po prostu odcinkiem stycznej i który definiuje odległość krzywej od asymptoty w każdym jej punkcie, staje się krzywą złożoną z dwóch części, jednej o krzywiźnie dodatniej (kiedy mieści się w przestrzeni o takiej krzywiźnie) i drugiej o krzywiźnie ujemnej (kiedy przebiega przez przestrzeń o krzywiźnie ujemnej). Nie jest możliwe połączenie odcinkiem prostej dwóch punktów leżących w dwóch przestrzeniach o przeciwnym znaku krzywizny. Pisałem o tym już w ostatnim akapicie rozdziału 6.3.

Do kłopotów dochodzi jeszcze sprawa terminologii, której niedostatek bywa bardzo często powodem nieporozumień. Kiedy piszę o prawie traktrysy, 2D lub 3D, mam na myśli układ krzywej i jej asymptoty razem, a nie tylko krzywej. Gdy piszę o liczbie wymiarów, również łatwo o nieporozumienie. W traktrysie oznaczonej jako 2D tylko krzywa jest dwuwymiarowa, jej asymptota jest jednowymiarowa. W „traktrysie 3D” jest to jeszcze bardziej skomplikowane, bo tylko asymptota jest trójwymiarowa, natomiast krzywa jest… czterowymiarowa. I w tym wypadku wcale nie chodzi o wymiar czasu klasycznego w czasoprzestrzeni Minkowskiego i Einsteina, nie chodzi o tzw. wymiary ukryte w teoriach strun, chodzi naprawdę o dodatkowy wymiar przestrzenny, wynikający z ujemności krzywizny samej traktrysy (bez asymptoty). Wygląda to, jakby ujemna krzywizna obiektu fizycznego powodowała w przestrzeni trójwymiarowej wzrost liczby jego wymiarów przestrzennych o jeden lub więcej. Poprzeczny przekrój asymptoty 3D, charakteryzującej się krzywizną dodatnią, kulistą, jest opisany jedynie promieniem okręgu, natomiast poprzeczny przekrój traktrysy w przestrzeni trójwymiarowej został przeze mnie opisany przez dwie przecinające się hiperbole, z których każda ma swoje odrębne parametry, mogące być zaliczone do „wymiarów”. Ta struktura zostanie graficznie przedstawiona w Części II.

Na ilustracji 9-3 jest pokazany szkielet do późniejszej konstrukcji modeli Wszechświata, zawierający traktrysy z asymptotami w przestrzeni trójwymiarowej. Po lewej stronie pokazałem samą zasadę budowy.

Zacznę od asymptoty. Jest to łuk o promieniu równym Φ, o kącie rozwarcia równym π oraz o grubości określonej przez okrąg o promieniu równym Φ^-4 (0,1459). Wymiar Φ^-4 został arbitralnie wybrany jako wyjściowy dla szkieletów wszelkich brył modeli o krzywiźnie dodatniej. Nie ma to jakiegoś wyjątkowego znaczenia, wymiary innych figur będą po prostu odniesione do wspólnego mianownika. Nas interesują jedynie proporcje. Asymptota o takim kształcie jest położona na płaszczyźnie układu współrzędnych prostokątnych (xy) tak, jak to już zrobiono na poprzednich ilustracjach w tym rozdziale. Jest oczywiste, że wszelkie wymiary odnoszące się do figur kosmicznych muszą być wyrażone zgodnie z kosmologicznym systemem liczbowym, który opisałem na wstępie tej opowieści w podrozdziale 2.1.

W części ilustracji po prawej stronie pokazane są 4 asymptoty, dwie na górze rysunku i dwie na dole. Każda z połówek mających kształt półokręgu występuje z drugą, będącą zwierciadlanym odbiciem pierwszej, tworząc w sumie figury kołowe. Oddzielność półokręgów zaznaczyłem różnymi kolorami, zbliżonymi do żółtego i beżowego. Asymptoty w dolnej części ilustracji, oznaczonej literą B, są zwierciadlanym odbiciem tych z części A, jednak obróconymi o kąt 90 stopni (π/2 = π/ Φ²-Φ^-1) wokół osi y. Proszę się nie zniechęcać rozwlekłością tego opisu, gdyż jest to okazja do przedstawienia zasady ortogonalności oraz zasady symetrii, które będą nam towarzyszyć w całej dalszej opowieści. Nie tylko te, równie ważną jest zasada współuwikłania par cząstek materii, wszelkiej materii, które biorą swój początek we wspólnej cząstce źródłowej (np. w wyniku wzbudzenia kwantowego i rozpadu tej cząstki), po czym ich fale prawdopodobieństwa rozchodzą się w przeciwnych kierunkach. Wspominałem o tym w podrozdziale 7.2.

Ważną zasadą rządzącą genezą i ewolucją Wszechświata jest zasada symetrii. Tę zasadę sformułowała nauka w kilku subtelnych znaczeniach o charakterze raczej matematycznym. Dla tej opowieści najistotniejsza jest ta część zasady, z której wynika, że w Wielkim Wybuchu masy i energie składników materialnych były dokładnie takie same. Jest to powodem, dla którego naukę trawi nieustannie pytanie: dlaczego w obserwowalnym Wszechświecie nie znaleziono antymaterii (ale można rzekomo ją wytworzyć w akceleratorach i zderzaczach) ani tzw. monopoli magnetycznych. Te składniki musiały być i to w takiej samej ilości energii/masy, a ich nie ma! Jeszcze jeden paradoks, jeszcze jedno niepewne twierdzenie w nauce. Stworzono więc teorię tzw. łamania symetrii i nadano im z czasem pozytywne znaczenia napędów ewolucji. W przeciwieństwie do nauki, w opowieści, czyli właściwie w rodzaju baśni, jest miejsce przede wszystkim na paradoksy i konstatacje „bajkowe”, przecież potrzebne są nie po to, żeby zastępować poznawczą rolę nauki, ale po to, żeby pobudzać wyobraźnię, bez której nauka jest martwa.

W kilku miejscach tej opowieści wspominam, że Wszechświat ma zdolności samoregenerujące po aktach „złamania symetrii”. Najłatwiej wyjaśnić to można na przestrzeni dwuwymiarowej, konkretnie na płaszczyźnie. W takiej przestrzeni możemy intropię przedstawić jako ortogonalne wektory, z których każdy leży w odrębnej ortogonalnej pragmacie, a więc podlega innej zasadzie przyczynowości, i których zwroty oznaczają kierunki wzrostu entropii (w nauce) albo wzrostu intropii termodynamicznej (w tej opowieści). Starałem się już to wyjaśnić w rozdziale 3. Zajmijmy się przypadkiem złamania symetrii wskutek utraty przez dwa składniki Wszechświata ortogonalności.

Proces ortogonalizacji wektorów w tzw. przestrzeni unitarnej jest matematycznie wyjaśniony w Wikipedii. Jako ogólny może się on wydawać nieco skomplikowany. W przypadku nieortogonalności dwóch wektorów intropii, z których każdy jest przyporządkowany odrębnej przestrzeni, a te przestrzenie, w rozpatrywanym teraz przykładzie, są określone przez płaszczyzny ortogonalne: jedna to płaszczyzna x–y (z=0), a druga x–z (y=0), proces ortogonalizacji będzie oczywistością. Każda z tych przestrzeni (por. ilustrację 9-4) reprezentuje odrębną ortogonalną „rzeczywistość”, czyli pragmatę.

Przypominam, że w rozdziale 3 wyjaśniałem subtelną różnicę między tymi dwoma pojęciami. Z tych wyjaśnień wynika, a przynajmniej powinno wynikać, że składowe ortogonalne każdego z wektorów, jeśli mają mieć sens fizyczny, mogą być rzutowane (projektowane) tylko na „swoje” pragmaty i te rzuty są właśnie zortogonalizowanymi wektorami intropii. Wynikające nieubłaganie z geometrii wektorowej pozostałe składowe obu wektorów reprezentują energie, które w „nie swoich” pragmatach zostają znihilowane, czyli zamienione na fotony ciepła i rozproszone, podnosząc temperaturę kosmicznego tła o jakiś niewyobrażalnie mały ułamek kelwina.

Będę do tych problemów jeszcze wielokrotnie wracał nie tylko z tego powodu, że są aksjomatami w tej opowieści, warunkują jej domniemywany sens, ale także dlatego, że nie jest łatwo wyjaśnić prawidłowo i zrozumiale ich istotę jako właściwość Przyrody na poziomie kwantowym, a zwłaszcza kiedy samemu ma się spore luki w zrozumieniu objaśnianych zjawisk. Przypomnę znane powiedzenie Richarda Feynmana: „Kto twierdzi, że zrozumiał fizykę kwantową, to znaczy, że niczego nie zrozumiał” oraz to, że sam Einstein uznał ją za „jakiś koszmar”.

Ilustracja 9-3. Próba wyjaśnienia budowy traktrysy dla przestrzeni trójwymiarowej. Z lewej strony pokazano warunek, że płaszczyzna, na której położona jest asymptota musi być ortogonalna względem płaszczyzny, na której jest położona krzywa traktrysy. Ta część ilustracji pokazana jest w rzucie perspektywicznym. Rysunki A i B pokazują ortogonalne pary układów traktrysa–asymptota. Wspólną podstawą dla obu par jest torus o promieniach Φ/1 (tzw. złoty torus). Płaszczyzna równikowa torusa dzieli całość na część górną A (można ją nazwać „północną”) i część dolną B („południową”).

Uprzedzając wyjaśnienia, w dalszych rozdziałach chciałbym jednak zaspokoić nasuwające się z pewnością pytanie: co pokazany na ilustracjach torus fizykalnie przedstawia i jaka jest jego rola? Torus, niekiedy ewoluujący w sferę, przedstawia wspólną dla obu części przestrzeń wypełnioną szczególnego rodzaju „materią”, która może istnieć tylko w warunkach ekstremalnych, opisywanych przez naukowców zajmujących się fizyką Wielkiego Wybuchu. Uprzedzam jednak, że w tej opowieści nie istnieje tak opisywane zjawisko, istnieje natomiast taka niby materia, którą będę nazywał plazmą o nieznanym stanie skupienia. Niektórzy autorzy nazywają ją „zupą kwarkowo – gluonową”, ja będę raczej unikał tak smakowitych określeń.

Traktrysa (niebieska krzywa) jest położona na płaszczyźnie układu współrzędnych xy tak, jak pokazano to na ilustracji 9-1. Tym razem krzywej nadano dodatkowe wymiary, do czego zmusza konieczność uwzględnienia ujemnej krzywizny, nie tylko wzdłuż krzywoliniowej osi symetrii podłużnej, ale także w przekroju poprzecznym. Krótko mówiąc: jeżeli rzutować trójkąt projektorem optycznym lub innym sposobem graficznym na powierzchnię „pogrubionej” traktrysy, to suma kątów w trójkącie, będącym rzutem w dowolnym miejscu i pod dowolnym kątem, musi być mniejsza od 180 stopni.

Z uwagi na to, że ilustracja 9-3 może niedostatecznie objaśnić ideę traktrysy 3D, zamieszczę jej inną wersję (w ukośnej perspektywie), pokazaną na ilustracji 9-4.

Proponuję uważną lekturę obszernego podpisu pod tą ilustracją, bo objaśnia ważne rozwiązania, które legły u podstaw niniejszej opowieści. Jak sądzę, możliwość jednoczesnego oglądu obrazu i odczytywania objaśnień znacznie ułatwi przyswojenie treści, co będzie konieczne w dalszej lekturze.

Ilustracja 9-4. Widok perspektywiczny obiektów z ilustracji 9-3 w ich normalnym wzajemnym położeniu. Kolorami wyróżniono cztery rodzaje traktrys, przewidzianych jako szkielety przyszłych obrazów intropii. Kolory czerwony i zielony będą wyróżniać intropię materii o grawitacji dodatniej (elksjomaterii), natomiast kolory błękitny i ciemnoniebieski intropię materii o grawitacji ujemnej (sprochnomaterii).

Ilustracja pokazuje przykład ortogonalności Wszechświata i jego składników. W tym celu pokazano także wzajemnie prostopadłe płaszczyzny, na których są położone figury krzywych i ich półkolistych asymptot.

Figury są sparowane: każda krzywa jest sparowana z jedną z asymptot leżącą na płaszczyźnie ortogonalnej, tworząc układy działające zgodnie z „prawem” traktrysy 3D. Ale to nie wszystko: pary traktrysa – asymptota, położone na tej samej stronie torusa podstawy (kolor ciemnozielony), są w stanie współuwikłania kwantowego, co oznaczę symbolem &. A więc będzie to uwikłanie typu 1&1, jedna para z drugą parą. Ponadto pary leżące na przeciwnych stronach torusa są także współuwikłane kwantowo, co zapiszę jako 2&2, czyli dwie pary traktowane jako całość z drugimi dwoma parami. Skomplikowane? Zapewniam, to tylko pierwsze wrażenie. Zadziwiającą właściwością „tego” Wszechświata jest jego prostota wynikająca tylko z kilku zasad. O niektórych napisałem już we wcześniejszych fragmentach głównego tekstu.

Ilustracja 9-5. Traktrysy i ich asymptoty w układzie ortogonalnym, o symetrii zwierciadlanej, widziane z frontu (1) i z boku (2). Dalsze wyjaśnienia w tekście.

Wyjaśniałem już ruchy punktów materialnych na traktrysie płaskiej i prostoliniowej asymptocie. Widzę potrzebę powtórzenia tych objaśnień na traktrysie 3D i w tym celu zamieszczam ilustracje 9-5.

Pokazałem widoki układu podwójnego (2&2), czyli dwóch układów traktrysa – asymptota, wzajemnie ortogonalnych. Rys. 2 powstał po przekręceniu rysunku 1 o 90 stopni wokół pionowej osi y. Z pewnością zwracają uwagę czerwone okręgi wmontowane w obie figury. Proszę się nie niepokoić, te okręgi, wszystkie o średnicy 1 (w moim komputerze 100), mają przekonać Państwa, że przedstawiona trójwymiarowa figura, uzyskana metodą cut and try, spełnia prawo traktrysy, któremu poświęciłem sporo miejsca w podrozdziałach 10.1 i 10.2. Proszę na razie się nie przejmować obecnością czerwonej sfery w dolnych częściach rysunków 1) i 2).

Prześledźmy ruchy pary sprzężonych ze sobą grawitacyjnie punktów materialnych na asymptocie i na traktrysie. Niech nasza podróż zacznie się w miejscu oznaczonym literą A. Sprzężony z tym punktem „partner” na traktrysie musi znajdować się (jeśli ma istnieć) na poziomie punktów B. Jeżeli cząstka w miejscu A chce kontynuować podróż w kierunku punktów B, to partnerzy z tych chwilowych lokalizacji muszą natychmiast uciekać na poziom C. Dalej odbywa się to tak samo. Meta dla obu cząstek jest na wspólnym poziomie D, a więc ta z nich, która inicjowała „wyścig”, dogoniła drugą, która przecież wystartowała z „forą”, równą średnicy jednego z kółek, czyli równą jedność. O ile szybkość liniowa punktu na asymptocie może być stała, to szybkość punktu na traktrysie maleje w miarę zbliżania się do „mety”, aby na samej mecie utracić w ogóle prędkość. W omawianym przykładzie mamy do czynienia z pchaniem cząstki na traktrysie przez odległą o 1 cząstkę na asymptocie. Możemy tę sytuację odwrócić, zaczynając od startu na poziomie D, a kończyć na poziomach A (asymyptota) i B (traktrysa). Taka kolejność byłaby dokładnym opisem spaceru z pieskiem, zamieszczonym na początku podrozdziału 9.1. Wtedy mamy do czynienia z ciągnięciem albo bardziej matematycznie wleczeniem cząstek na traktrysie przez cząstki na asymptocie.

Wszystko to, co opisałem w rozdziale 9, nie jest tylko geometryczną ciekawostką. Wspomniałem już na początku, że zmaganie się pary cząstek o takiej samej masie, ale o przeciwnym znaku grawitacji, prowadzi do gromadzenia się wzdłuż promienia układu ogromnych energii, które mogą „ożywić” Wszechświat. Stąd tytuł rozdziału.

Pozostaje do pilnego wyjaśnienia jeszcze jedna ważna sprawa, a mianowicie sprawa ujemnej krzywizny traktrys na zamieszczonych wyżej ilustracjach 9-4 i 9-5. Uważny czytelnik z pewnością spostrzegł, że przekroje poprzeczne traktrys (błękitnych i niebieskich) są inne niż u asymptot (czerwonych i zielonych). Figurę 3D, a także zajmowaną przez nią przestrzeń, można określić jako charakteryzujące się krzywizną ujemną dopiero wtedy, gdy ta figura zachowuje tę ujemność w obu jej ortogonalnych przekrojach. Traktrysy 3D, które uzyskały trzeci wymiar przez nadanie im grubości, nie mogły mieć przekroju kołowego (tak, jak asymptoty), który z definicji ma krzywiznę dodatnią. Rozwiązaniem okazały się dwie przecinające się hiperbole, natomiast homogeniczność krzywej zamkniętej, niezbędną z powodów graficznych, uzyskano ze „srebrnej” elipsy (tzn. o stosunku dużej i małej półosi równym Φ²⁾ przez jej zagięcie wokół jednej z osi współrzędnych, w ilustrowanym przykładzie była nią oś y. Pokazano to na ilustracji 9-6.

W atlasach astronomicznych można napotkać fotografie wyjątkowych mgławic, nazwanych „Ciemnymi”, ponieważ można je zlokalizować jako czarne plamy w kształcie rogalika, interpretowane jako rejony, z których nie dociera do nas wykrywalne światło. Wiele z tych ciemnych mgławic (np. pokazana na ilustracji 9-7 mgławica Barnard 68) bardzo przypomina kształt przekroju strumienia materii o grawitacji ujemnej, znany z ilustracji 9-6 i innych.

Ilustracja 9-6. Uzyskanie homogenicznej krzywej zamkniętej, o krzywiźnie ujemnej na większości konturu figury. Fragmenty oznaczone żółtym kolorem nie mają praktycznego znaczenia w pokazanych dalej modelach Wszechświata.

Ilustracja 9-7. Ciemna mgławica Barnard 68

Wszystko to, co opisałem w rozdziale 9 nie jest tylko geometryczną ciekawostką. Wspomniałem już na początku, że zmaganie się pary cząstek o takiej samej masie, ale o przeciwnym znaku grawitacji, prowadzi do gromadzenia się w ich otoczeniu (cokolwiek by ono znaczyło) ogromnych zasobów energii potencjalnej, która może poruszyć Wszechświat, nie tylko pod względem kinetycznym, ale także strukturalnym. Oceniam z pewną dozą niepewności, że przy założeniu, że każda z materii, jakie wchodzą w skład Wszechświata, wnosi energię tylko w ok. 4,5 % energii całkowitej, udział sumarycznej energii potencjalnej, wynikającej z istnienia obu rodzajów grawitacji, wyraża się liczbą 72 %, a może nawet 76 %, nie wliczając w to energii i fotonów, i informonów. Stąd tytuł rozdziału.

1.10 Bezmasowy foton to fikcja.

A więc stało się, wraz z tym „jubileuszowym” podrozdziałem moja opowieść oznacza jawny sprzeciw wobec nauki akademickiej ze strony „oszołoma”, a nawet „oszusta”. Jest oczywiste, co może zrobić naukowiec, który fatalnym zrządzeniem losu natrafił na tę książkę i do tego miejsca doczytał: po prostu ją odrzuci z jeszcze jednym przekonaniem, że Internet jednak poprzewracał ludziom w głowach.

Ale chwileczkę, Panie i Panowie Doktorzy, mam prawo do obrony. Są precedensy uznanych fizyków i pedagogów akademickich, którzy osiągnąwszy wiek „dojrzały +”, radzi by wyrzucić z nauki niektóre z balastów, pochłaniających cenne środki materialne i osobowe, bez których nauka będzie nadal sobie radzić, może nawet jeszcze lepiej. Prosicie o przykłady? Proszę bardzo.

Zechcecie Państwo sięgnąć w przód do ostatniego akapitu podrozdziału 11.1. Wzmiankowana tam książka to długi, ale nie nudny, dialog Profesora (Jean-Pierre’a Lasoty) z Dziennikarką (Karoliną Głowacką), zainteresowaną współczesnymi problemami fizyki i kosmologii. Znakomity pomysł z każdego punktu widzenia. J-P Lasota jest emerytowanym profesorem Instytutu Astrofizyki w Paryżu, profesorem wizytującym w Centrum Naukowym imienia Mikołaja Kopernika w Warszawie, uczonym, który nie skrywa swoich radykalnych poglądów. Nie będę posługiwał się dosłownymi cytatami z książki, a jedynie ich streszczeniem, za które to ja biorę odpowiedzialność.

Skrzydeł dodała mi wypowiedź Profesora, że jeśli chodzi o teorię grawitacji kwantowej, czyli najważniejszego od wielu lat kierunku poszukiwań fizyki teoretycznej i matematyki, to właściwie nie wiadomo, czy jest ona naprawdę potrzebna. Brak jest jakichkolwiek danych doświadczalnych czy obserwacyjnych, które by wymuszały jej opracowanie. Potrzeba takiej teorii jest potrzebą bardziej filozoficzną niż warunkującą rozwój fizyki.

Uff, co za ulga… Ja z tytułem podrozdziału powyżej w tej sytuacji jawię się jako zwykły oportunista, zwłaszcza kiedy dopowiem, że z wyrażonym poglądem Profesora zupełnie się nie zgadzam. Prawdopodobnie można doskonale uprawiać fizykę, nie wiedząc, co jest wewnątrz czarnej dziury (tak przynajmniej twierdzi Pan Profesor), ale bez teorii grawitacji kwantowej nie może zostać wyjaśniony Wszechświat jako całość, razem ze mną i Panem Profesorem, jako jego, Wszechświata, integralnymi cząstkami. Choćby z takiego powodu, że czarne dziury są bytami przede wszystkim medialnymi, zadaniem Wszechświata jest tylko możliwie szybka ich likwidacja jako patologii Kosmosu, poza tym nie mają większego znaczenia. Są tworem „patologicznym”, bo naruszają symetrię Wszechświata i na likwidację powstałej asymetrii trzeba stracić trochę cennej energii. Mają urok chyba tylko dla entuzjastów tuneli czasoprzestrzennych i autorów scenice-fiction. Już samo to, że do ich naukowego opisu potrzebne okazuje się pojęcie „osobliwości”, powinno być ostrzeżeniem: nie tędy droga! Wyrzućmy więc te „czarne dziury” jako naczelną, medialną, „prawdę o Kosmosie”, nie oszczędzając nawet tych „bez włosów”, według pomysłu Stephena Hawkinga. Czy zgodzi się Pan z tym, Panie Profesorze Lasota?

Skoro upewniłem się, że jestem w doborowym towarzystwie odważnego i utytułowanego radykała, przejdę do fotonu. Od ponad 100 lat do dzisiaj obowiązuje w nauce pogląd, że masa spoczynkowa kwantu światła, obojętnie, czy mającego postać fali elektromagnetycznej, czy „bezmasowej” cząstki, jest równa zero. Zauważcie Państwo, proszę: „zero” okazuje się tutaj dopuszczalnym bytem kwantowym…! Fizyka kwantowa nie może obejść się bez „stałej” c. Foton ma energię, wyznaczoną przez jego częstotliwość ze współczynnikiem proporcjonalności równym stałej Plancka. Ma także pęd, który „normalnie” jest iloczynem masy i prędkości cząstki, ale że fotonowi rzekomo brakuje masy, to wymyślono: moment pędu fotonu jest ilorazem stałej Plancka i długości fali światła. A jaka jest szybkość fotonu? Jedyna, jakże żałosna odpowiedź to: szybkość fotonu w próżni jest równa szybkości światła w próżni. To znaczy ile? Z podrozdziału 10.1 wynika, że właściwie nie wiadomo. Taką wiedzę mają natomiast eksperci NIST, skoro ją publikują jako stałą absolutną. A czy w ogóle może być wiadomo, ile ta szybkość wynosi? O tym napiszę w następnym podrozdziale.

Można by mnożyć przykłady, często zapamiętane bezkrytycznie ze szkoły średniej albo wyższej, świadczące tylko o tym, że fizyka, jako nauka akademicka, ugrzęzła w bezkrytycznej interpretacji doktryny znanej jako Szczególna Teoria Względności (STW ) i nie może się z niej wydostać, sprawiając sama sobie wielką liczbę paradoksów. Pytanie: dlaczego taka skłonność do doktrynerstwa ma miejsce w środowiskach naukowych, niejako z definicji otwartych na inność i nowość, to pytanie, na które może być odpowiedź bardzo „naukowa”, ale ja skłaniam się do uproszczenia: w warunkach dominacji autorytetów żyje się łatwiej, z pewnością bez lęku przed prawdą. W rozpatrywanym przypadku interpretacji STW najdotkliwszą cenę za pozycję ostatecznego autorytetu zapłacił sam Einstein: utracił bliskich, aktywnie się do tego przyczyniając, stał się bardziej celebrytą niż niezależnym uczonym (proszę porównać jakże wtedy prymitywne media lat 20. i 30. z tymi XXI-wiecznymi) i choć dostał Nagrodę Nobla za kwantowe wyjaśnienie efektu fotoelektrycznego, to później sam stał się konserwatystą w rozwoju fizyki kwantowej. Nie ma czego zazdrościć Wielkim Autorytetom. To nie ich wina, raczej spójrzmy po sobie, bo to my w lęku przed prawdą ich kreujemy.

„Umasowienie” fotonu właściwie rozwiązywałoby wiele niejasnych problemów. Nie godziłoby w jego falowość, bo nie tylko fotony mają dualną naturę. Wszystko, co nas otacza, także taką ma, z nami, ludźmi, włącznie. Sprowadziłoby dyskurs na temat prędkości światła na logiczne tory, takie jak dla wszystkich innych cząstek materialnych Modelu Standardowego. A najważniejsze w tym dyskursie: dostarczyłoby podstaw zarówno teoretycznych, jak i w przyszłości doświadczalnych, obalających, nieuzasadnioną, moim zdaniem, tezę Einsteina o niezmienności szybkości światła emitowanego ze źródła ruchomego.

Nie jestem pierwszym, który takie poglądy głosi. W latach dziewięćdziesiątych XX wieku ukazało się kilka publikacji mało znanych ośrodków naukowych, w których autorzy szacowali masę spoczynkową fotonu między 10^-16 a 10^-27 eV/c². Wspólną cechą tych niepewnych źródeł było to, że nie wiązano masy fotonu z jego energią potencjalną, czyli z częstotliwością ν, co w tej opowieści okaże się niesłuszne.