OPOWIEŚĆ KOSMOLOGICZNA

autor: Janusz Bator

Część III

Stała struktury subtelnej „alfa”, podstawowa stała
pankosmiczna

Spis treści podrozdziałów

Tytuły są podlinkowane. Wystarczy kliknąć, aby przenieść się bezpośrednio do wybranego podrozdziału.

3.2 Zaskakujące implikacje w kwestii materii w ruchu i dynamiki ewolucji.

3.3 Co ma wspólnego stała alfa z „mrocznym urokiem światła”? Czy jest kłopot z STW?

3.4 Znikoma zmienność wartości liczbowej α. Wielki sukces astrofizyków doświadczalnych i ambitne wyzwanie dla teoretyków.

3.5 „OPERA” w Gran Sasso (2011 r.) to może nie „finalna aria” „tragikomicznej opery”, ale raczej uwertura?

3. 1 Co mówi nauka?

O istnieniu takiej stałej dowiedziałem się z czasopisma „Newsweek” z 16.10.2010 r., z artykułu pani Bożeny Kastory, pod przykuwającym uwagę tytułem: „Największa cholerna tajemnica fizyki” (https:/www.newsweek.pl/wiedza). Autorka napisała m.in.:

„Jeden z najwybitniejszych fizyków XX wieku, Richard Feynman, nazwał ją „liczbą magiczną”, a także „jedną z największych cholernych tajemnic fizyki”. Z obliczeń fizyków wynikało bowiem, że gdyby jej wartość była odrobinę mniejsza lub większa, cały wszechświat zmieniłby się dramatycznie. Inaczej zbudowane byłyby gwiazdy; galaktyki formowałyby się w inny sposób; atomy pierwiastków miałyby inne powłoki elektronowe wokół jąder, a zatem i inne właściwości. Prawdopodobnie i życie na Ziemi miałoby inny charakter albo nie powstałoby wcale. Zrozumienie, dlaczego nawet minimalna zmiana wartości tej liczby mogłaby zmienić całą architekturę wszechświata, dla wielu fizyków stało się pasją życia.”

Czy trzeba więcej, żeby ulec takiej pasji? Uległem jej i ja przystępując do snucia tej opowieści. Niestety, materiały na ten temat okazały się dość skromne, często powtarzały się określenia „tajemnicza stała fizyki”. Przełomową lekturą okazał się dla mnie artykuł Johna D. Barrow’a i Johna K. Webb’a pt. „Niestałe stałe” („Shifting Universal „Constants” Could Reveal Space’s Hidden Dimensions”) w wydaniu specjalnym Scientific American w całości poświęconym tematowi „Czym jest czas” (Świat Nauki nr 11, wrzesień – październik, 2012). Nie zamierzam przytaczać tu wszystkich rewelacji autorów, wytrawnych badaczy stałych przyrody, ale o niektórych z nich muszę szerzej wspomnieć.

Wzór na stałą alfa (α) sformułował w 1916 r. Arnold Sommerfeld, pionier zastosowań mechaniki kwantowej do teorii elektromagnetyzmu, jako prostą („elegancką” powiedzieliby naukowcy) zależność matematyczną:

gdzie e jest ładunkiem elektrycznym pojedynczego elektronu, ε₀ przenikalnością elektryczną próżni, h stałą Plancka i c szybkością światła w próżni.

Wzór określa relatywistyczne (c) i kwantowe (h) własności cząstek z ładunkiem elektrycznym (e) w próżni (ε₀), ponadto jest liczbą bezwymiarową, co sugeruje możliwość jej pankosmicznego zastosowania. Zgodnie z najnowszymi pomiarami (por. tabele CODATA) wartość stałej α₀ jest równa 0,007 297 352 566 4 z niepewnością ± 17×10^-8 , czyli w innym, nieco wygodniejszym zapisie 1/137,035 999 76.

Według angielskiej Wikipedii dokładność wyznaczenia stałej α wynosi (obecnie?) 0,25 x10⁹, czyli niedokładność występuje dopiero na 9-tym miejscu po przecinku. Według innych źródeł: 46 x 10-8, czyli jest znacznie większa, występuje już na 6-tym miejscu po przecinku, co byłoby bliższe danym na ilustracji 12-1. Prawdopodobnie jest to niedokładność pomiaru, ale jak się wkrótce okaże, nie tylko.

Nie wiadomo czym się kierował Sommerfeld formułując ten wzór, niewątpliwym faktem jest jednak, że jego intuicja przekroczyła wszelkie możliwe oczekiwania. Okazuje się bowiem, że (jak piszą autorzy wspomnianej publikacji) gdyby α miała nieco inną wartość, zmieniłoby się wiele zasadniczych cech otaczającego nas świata.

Autorzy wymieniają wiele skutków zachowania stałej α. Przytoczę dla przykładu jeden: zmiana wartości tej stałej o zaledwie 4% przesunęłaby poziomy energetyczne jąder atomów węgla w takim stopniu, że w gwiazdach ustałaby produkcja tego pierwiastka. Gdyby z kolei ta wartość przekroczyła 0,1 synteza jądrowa byłaby niemożliwa. Sommerfeld jak się zdaje nie przypuszczał, że sformułował warunek istnienia nie tylko Wszechświata, ale zapewne także całego wielowszechświata.

Ale to jeszcze nie wszystkie rewelacje związane ze stałą α.

Wieloletnie badania autorów oraz Victora V. Flambauma z University of New South Wales w Australii i innych, przeprowadzone na dwóch różnych wielkich teleskopach (VLT w Chile i Keck na Hawajach), doprowadziły do zaskakujących wyników. Okazuje się, że α nie jest idealnie stała, podlega minimalnym wahaniom na 6-tym miejscu po przecinku w wartości CODATA przywołanej wcześniej w tym podrozdziale. Oznacza to, że te odstępstwa od wcześniej ustalonej wartości, uznanej za pewną, są rzędu jednej dziesięciotysięcznej procenta. Mało tego: największe odchyłki α mają miejsce wzdłuż pewnego kierunku przestrzeni Wszechświata obserwowalnego. Na zamieszczonej niżej ilustracji 12-1, zaczerpniętej z opisywanego artykułu, ten kierunek zaznaczono niebieską linią, usytuowaną pod kątem około 45 stopni względem osi x. Można by przypuszczać, że autorzy znali tę oś, jako wyznaczoną przez położenie płaszczyzny równika, ale to nie takie proste. Surfując w przestrzeni Wszechświata nie wiemy, gdzie są „proste” albo okrąg określające położenie tej płaszczyzny. Nie dysponujemy jakimikolwiek racjonalnymi danymi, żeby stworzyć na swój użytek globalny układ współrzędnych ortogonalnych, no może z jednym wyjątkiem: płaszczyzny dysku naszej Galaktyki. Rozwiązanie zagadki położenia wspomnianej linii jest proste: obserwatoria ESO w Keck na Hawajach i VLT w Chile mają korzystne dla wielu eksperymentów współrzędne, ich szerokości geograficzne (lattitude) różnią się o 44026’, natomiast długości geograficzne (longitude) różnią się o 85004’.

Dzięki misji satelity Planck, jeśli moje dalsze wnioski przedstawione w podrozdziale 12-4 są słuszne, możemy się z grubsza orientować, jaka jest nasza pozycja względem umownej osi każdej z połówek Wszechświata, będącej krzywą najkrótszego połączenia bieguna N z centralnym punktem koła równikowego.

To już dużo, nawet bardzo dużo, ale jak w takim razie znaleźć ten wyróżniający się kierunek, o którym piszą autorzy publikacji? A jednak znaleźli i zmierzyli amplitudy odchyłek wartości stałej α z niewiarygodną dokładnością 10^-4 %. Dzięki temu odkryciu wiemy także, że lokalne zmiany wartości stałej są niezwykle powolne. Jedno z cyklu badań doprowadziło badaczy do wniosku, że w ciągu ostatnich 2 miliardów lat stała alfa nie zmieniła się więcej, niż o jedną stumilionową (10^-6 %). Badania innych badaczy w innych warunkach potwierdziły powolność zmian: w czasie, gdy tworzyły się meteoryty i składniki Układu Słonecznego (czyli ok. 4,5 miliarda lat temu), wartość alfa nie różniła się od wyznaczonej obecnie więcej, niż o dwie milionowe (2×10^-4 %).

Są to spostrzeżenia niezwykłe z racji wagi zawartych w nich informacji, o fundamentalnym znaczeniu dla dalszego postępu kosmologii. Godne podziwu i najwyższego szacunku jest to, że w te pomiary, niezwykle subtelne, zaangażowane były zespoły z licznych i rozsianych na naszym globie uniwesytetów Sankt Petersburga, Harvardu, Princeton, Kolumbii Brytyjskiej i innych ośrodków naukowych, oraz w wielkich obserwatoriach Kerck na Hawajach i VLT w Chile. Współpraca i organizacja (albo samoorganizacja) tych badań skłania mieszkańca Europy do refleksji. Jeśli dalsze badania potwierdzą osiągnięte wyniki, trzeba je będzie uznać za należące do najważniejszych odkryć przełomu XX i XXI wieków i można mieć nadzieję, że zostaną kiedyś uhonorowane jakąś zbiorową Nagrodą Nobla.

3. 2 Zaskakujące implikacje w kwestii materii w ruchu i dynamiki ewolucji.

Teraz przyszedł czas na pytania:

*) czy zaproponowany model Wszechświata uzasadnia wyróżnienie jakiegoś kierunku w jego przestrzeni, wzdłuż którego amplituda zmian wartości α byłaby w jedną stronę rosnąca, a w drugą, przeciwną malejąca? To pytanie jest szczególnie ważne, ponieważ nauka od co najmniej dwóch dekad uparcie podtrzymuje twierdzenie o jednorodności i izotropii Wszechświata;

**) czy zaproponowany model Wszechświata wyjaśnia, jaki jest właściwie sens fizyczny wzoru Sommerfelda podanego na wstępie tego podrozdziału, a nie tylko sens matematyczny? A przecież odpowiedź na to pytanie jest sednem „tej cholernej tajemnicy fizyki”.

Ilustracja 12-1. Przesunięcie alfa. Rysunek zaczerpnięty ze Świata Nauki. Wydanie specjalne. Nr 11, 2012.

Ilustracja 12-2. Przykład linii pseudogeodezyjnych na różnych „głębokościach” wewnątrz bryły jednej z elksjomaterii po jej skręceniu o 90 stopni wzdłuż linii N-S. Widok z frontu.

Ilustracja 12-3. To samo, co na ilustracji 12-2, widok z góry

Zacznijmy od pytania pierwszego, drugie zasługuje na poświęcenie mu osobnego podrozdziału. W geometrii euklidesowej znane jest pojęcie linii geodezyjnych, w skrócie nazywanych po prostu „geodezyjnymi”. Dla tej opowieści wystarczy, jeśli przypomnę, jak najkrócej definiuje te linie Wikipedia:

„Linia geodezyjna (krótko nazywana geodezyjną) – krzywa w przestrzeni metrycznej (ściślej: w G-przestrzeni), stanowiąca najkrótszą drogę pomiędzy dwoma punktami dostatecznie bliskimi.”

Teoria geodezyjnych jest rozbudowana, dotyczy wielu rodzajów przestrzeni, o różnej krzywiźnie i z braku solidnej wiedzy nie podejmuję się tutaj jej wykładania, zwłaszcza, że dalsza część opowieści tego nie wymaga. Wprowadzę natomiast (wyłącznie dla potrzeb tej książki) pojęcie ”pseudo geodezyjnych” w przestrzeni trójwymiarowej. Będzie do tego potrzebne światło.

Przez pseudogeodezyjną będę rozumiał najkrótszą trajektorię fotonów przelatujących z jednego punktu przestrzeni do innego dowolnego punktu tej przestrzeni, jeśli warunki grawitacyjne i inne pozwalają na zapewnienie ciągłości tej trajektorii. O tym, czy wybrana przez fotony trajektoria jest istotnie najkrótsza wśród innych możliwych, decydują one same, w myśl zasady minimum energii potencjalnej.

„Zasada minimum energii potencjalnej jest wyznacznikiem kierunku procesów zachodzących w układach fizycznych. Zgodnie z nią dowolny układ będzie zmniejszał swoją energię potencjalną zawsze, gdy tylko będzie to możliwe, tzn. gdy będzie miał możliwość oddania nadmiaru energii oraz gdy nie będą na niego działały zbyt duże zakłócenia, uniemożliwiające ten proces.” (Wikipedia).

Warto też mieć na uwadze, że pojęcie minimum energii potencjalnej w tej zasadzie dotyczy minimum lokalnego, a nie globalnego. W opisywanym wypadku oznacza to autonomiczność poszczególnych pseudogeodezyjnych.

Takie rozumienie zaproponowanego terminu prowadzi do wniosku, że jeśli źródło fotonów znajduje się na biegunie S lub N, to światło emitowane z tych biegunów może dotrzeć do każdego punktu wewnątrz trójwymiarowego Wszechświata, co z kolei oznacza, że z każdego punktu można poprowadzić do obu biegunów krzywe odpowiadające sformułowanej tu definicji pseudogeodezyjnych.

Na ilustracjach 12-2 i 12-3 przedstawiono bryłę intropii materii „zwykłej”, czyli koinomaterii w fazie szczytowej ekspansji całego Wszechświata. Bryła ta, jak wiadomo z poprzednich wyjaśnień i ilustracji, ma kształt stożka, zagiętego wokół osi o kąt 90 stopni. Ale to nie wszystko, Wszechświat jest bardziej skomplikowanym bytem.

Z powodów, które wyjaśnię w dalszych podrozdziałach, materia, każda materia, nie opada na przyciągającą ją gwiazdę wzdłuż najkrótszych łączących je łuków. „Obłoki” intropii materii, w miarę jej ekspansji od fazy eksflacji do fazy szczytowej tej ekspansji, czyli w miarę opadania na przyciągającą je gwiazdę, podlegają skręcaniu (twist).

W proponowanych tu modelach kąt skrętu wynosi 90 stopni.

Na razie przypomnijmy tylko, że znamy podobne zjawisko z codziennego życia w postaci okręgów wirującego strumienia wody wypływającej z wanny albo umywalki, o coraz mniejszym promieniu wiru i coraz większej prędkości obwodowej. Znane są także inne zjawiska potwierdzające, że mamy tu do czynienia z przejawem znanych w Kosmosie i na Ziemi praw fizyki, np. zjawisko wiru akrecyjnego. Ale bywają również inne, znane z życia efekty skręcania się strumienia materii, o odpowiednio dobranych własnościach, takich, jak lepkość. Proszę przypatrzeć się uważnie cienkiemu, pionowemu strumieniowi miodu przelewanego z jednego naczynia do drugiego. Powstający na dole strumienia stożek wiru nie został, jak się wydaje, wyjaśniony dotychczas przez naukę. Wzmiankowałem o tym już w rozdziale 8.4.

Wraz ze skręcaniem bryły intropii skręcają się o taki sam kąt wszystkie pseudogeodezyjne. Pokazałem to na ilustracjach 12-2 i 12-3. Ilustracja 12-3 ma przekonać oglądającego, że wewnątrz tego samego zagiętego stożka znajduje się nieskończona, a przynajmniej nieobliczalna ilość pseudogeodezyjnych dla różnych, w nieobliczalnej ilości, pozycji miejsc obserwacji.

Jak napisałem kilka akapitów wcześniej, z dowolnie wybranego punktu w Kosmosie można poprowadzić unikalną, jedną jedyną pseudogeodezyjną z bieguna N lub S do centrum koła równikowego.

Niech na ilustracji 12-3 czerwona mała sfera oznacza miejsce obserwacyjne zmian stałej α. Pamiętajmy, że ta mała kuleczka może mieścić naszą Galaktykę, Układ Słoneczny, a więc i naszą Ziemię i wreszcie szacowną grupę badaczy z ich aparaturą. Jedno jest pewne: przez ten „punkt obserwacyjny” przebiega trajektoria fotonów między biegunami N i S (a „po drodze” przez centrum koła równikowego), spełniająca zasadę minimum energii potencjalnej.

Wspomniani tu badacze mierzą amplitudy zmian stałej α wzdłuż jedynej trajektorii, jaka jest dla nich dostępna, czyli wzdłuż pseudogeodezyjnej, przy czym mogą to robić dla różnych odległości od jądra Ziemi, mierzonych w stronę bieguna N (albo S) i centrum koła równikowego. Z artykułu i przytoczonego rysunku nie wynika bezpośrednio, w którym kierunku dane odchyłek α zbliżają się lub oddalają względem biegunów lub równika. Ta kwestia zostanie rozstrzygnięta w dalszej części tego opracowania. Na razie musi wystarczyć następujące spostrzeżenie, bez znaczenia jednak na wniosek końcowy.

Wprawdzie umówiliśmy się dużo wcześniej, że wewnątrz bryły zagiętego stożka gęstość intropii jest stała (uśredniona), to jednak nie jest to tożsame ze stałością gęstości materii. Jest, mam nadzieję, oczywiste, że w miarę zbliżania się do bieguna gęstość materii o grawitacji dodatniej rośnie, a wraz z nią rośnie jej temperatura. Odwrotny proces ma miejsce dla odległości i grawitacji ujemnych. Można tylko intuicyjnie przewidywać, że większym wartościom gęstości i temperatury towarzyszą większe amplitudy wahań wartości stałej α, mniejszym mniejsze wahania. Zarówno gęstości, jak i temperaturze towarzyszą niemożliwe do uniknięcia fluktuacje tych wielkości, które przekładają się na niezwykle małe, ale wykrywalne wahania wartości stałej α. Przypomnę: na 6-tym miejscu po przecinku! Nie ufajmy jednak intuicji jeśli brakuje wsparcia doświadczalnego lub matematycznego.

3. 3 Co ma wspólnego stała alfa z „mrocznym urokiem światła”? Czy jest kłopot z STW?

Zastanówmy się nad fizycznym znaczeniem niektórych jednostek Plancka. Znaczenie długości Plancka i szybkości światła zostały wcześniej objaśnione, chociaż wartości liczbowe tej drugiej budzą wątpliwości. Problemem ważnym w dalszym ciągu tej opowieści są: temperatura Plancka T_p i masa Plancka m_p.

Jeśli chodzi o temperaturę Plancka tym problemem są pytania: czy temperatura Plancka jest krytyczną temperaturą plazmy w takiej fazie jej termicznej ewolucji, kiedy może nastąpić zmiana pragmy na „antypragmę”, czyli taką, w której wszystkie cztery stygmaty czasu zmieniają swoje zwroty na przeciwne?

Jeśli tak, to czy taka wartość liczbowa towarzyszy pragmatropii przy narodzinach każdego kolejnego cyklu ewolucji wielowszechświata?

Czy taka wartość temperatury Plancka ma jakikolwiek związek z warunkami termicznymi we Wszechświecie obserwowalnym?

Temperatura Plancka według oficjalnych danych naukowych wynosi: T_p= 1,416 808 x 10³²K, co w moim przekładzie na kosmiczny system liczbowy wynosi Φ^153,950293K.

Nasuwa się przypuszczenie, że jeżeli średnia temperatura tła w „naszym” Wszechświecie, zmierzona przez trzy kolejne misje satelitarne: COBE, WMAP i PLANCK doprowadziły do wartości T_CMB= 2,72548 K (Φ^2,083 ⁵⁸³ K), przy czym niepewność wartości zmierzonej ocenia się na ±570 μK, czyli ±2,1 x10^-2 %, to musi istnieć jakiś związek T_CMB z T_P.

W kosmologii nie jest to imponująca dokładność, ale trzeba wziąć pod uwagę, że misja Planck ujawniła także niewielką, ale liczącą się niejednorodność rozkładu promieniowania rzędu 10^-5. Może to i mało, ale nie upoważnia jeszcze moim zdaniem do twierdzenia, że obowiązujący model kosmologiczny Lambda CDM nadal nie wymaga korekty. Trochę wygląda to na naginanie faktów do przyjemnego wydarzenia. Nawiasem mówiąc dane, jakie przytoczyłem w poprzednim podrozdziale (ilustracja 11-2) świadczą, że Wszechświat jest nie tylko niejednorodny, ale również anizotropowy. Anizotropowość wynosi też ok 10^-5. Przypadek?

Następne wątpliwości dotyczą masy Plancka. Masa Plancka, wydaje się zbyt duża, jak na wielkość kwantową, a komentarze naukowe do tego parametru są ogólnikowe. Wynosi ona m_p = 2,17645 x 10^-8kg, a odpowiadająca jej energia Plancka jest równa E_P = m_p x c² = 1,9561 x 10⁹ J. Na razie ignoruję to, że zamiast c powinna występować stała proporcjonalności między masą i energią, którą oznaczyliśmy jako stałą świetlną C₀. Wrócę do tego jeszcze w tym rozdziale.

Jeżeli temperatura Plancka T_P jest warunkiem koniecznym do uruchomienia procesu pragmatropii, to jest sprawą podstawową, jaka energia jest do tego niezbędna. W następnym rozdziale (patrz tekst i ilustracja 12-2) dowiemy się, że według tej opowieści energia pierwszego cyklu ewolucji Wszechświata musi wystarczyć na istnienie i ewolucje wszystkich pozostałych cykli wielowszechświata. Nic więc zaskakującego w tym, że zasada minimum energii potencjalnej, znana już z podrozdziału 3.2, jest w ewolucji Wszechświata przestrzegana rygorystycznie.

Przyjęta tutaj interpretacja temperatury Plancka, jako stałej fizycznej oraz liczne obliczenia, trochę przypadkowo doprowadziły mnie do odkrycia zaskakującego, jeszcze jednego fizycznego znaczenia i roli stałej α. Oto to „odkrycie”:

Stosunek temperatury Plancka, najwyższej możliwej temperatury w procesie pierwszej i każdej następnej pragmatropii, do temperatury promieniowania tła (T_CMB), do której następuje schłodzenie plazmy po zakończeniu pragmatropii, czyli na starcie do pierwszego cyklu wielowszechświata, jest równy Φ^1/α. Cóż to jest ta temperatura tła? Dlaczego ma ona, jako fizyczna wielkość liczbowa, tak duże znaczenie w kosmologii, a przynajmniej w tej nienaukowej hipotezie, będącej tematem Opowieści?

Powodem jest druga zasada termodynamiki (DZT), której interpretacja w literaturze bywa różna, co nie znaczy błędna, lecz prowadząca do nieporozumień. Takim nieporozumieniem jest zagrożona definicja T_CMB. Pamiętajmy, że T_CMB nie jest stałą, jest natomiast wielkością charakteryzującą fazę w danym cyklu ewolucji, a więc zmienną.

Schłodzenie plazmy pragmatropowej i spadek jej temperatury z T_P do temperatury T_CMB termodynamika niekiedy interpretuje, jako „osiągnięcie stanu równowagi cieplnej”, najbardziej prawdopodobnego stanu makroskopowego. Ta równowaga jest także stanem o największej „entropii” (patrz Lee Smolin: „Czas odrodzony. Od kryzysu w fizyce do przyszłości Wszechświata”. Tłum. Tomasz Krzysztoń. Prószyński i S-ka. 2015). I w innym miejscu: „entropia rośnie, gdy liczba informacji (o zachowaniu cząstek) maleje, i na odwrót”. Taka jest właśnie istota równowagi termodynamicznej.

Czytelnik tej opowieści wkrótce się dowie, a być może już o tym wie, że w przedstawionej koncepcji ewolucji Wszechświata, a właściwie wszechświatów, jest dokładnie odwrotnie. Czy to ma znaczyć, że DZT jest błędna? Zaprzeczam kategorycznie, ale zwracam uwagę, że autorzy zdają się niekiedy pomijać obecność i oddziaływanie grawitacji, a więc rozważać entropię w środowisku bardziej złożonym i przez to całkowicie odmiennym. Musimy odróżnić równowagę termodynamiczną w książce wybitnego fizyka od równowagi termicznej, której istotą jest wyrównanie temperatur ciał we wspólnym środowisku, co nie jest równoznaczne ze stanem, w którym zrównoważone są wszystkie siły i nie ma przepływu materii ani reakcji chemicznych. Intropia, w odróżnieniu od entropii termicznej, nie jest tylko skutkiem procesów cieplnych, ale także efektem współdziałania jeszcze innych oddziaływań, przede wszystkim elektromagnetycznych i grawitacyjnych. Temperatura promieniowania tła po zakończeniu pragmatropii osiąga swoją wartość liczbową nie tylko w wyniku uzyskania równowagi termicznej, a więc także intropii termicznej, ale także innych oddziaływań, co każe nam przydawać intropii przymiotnik „termodynamiczna”.

Schłodzenie plazmy do stanu, w którym przyjmuje ona już postać materii o temperaturze struktur w otaczającej przestrzeni nie oznacza, że ta schłodzona materia osiągnęła maksimum swojej entropii, czyli nieuporządkowania, a tym samym minimum posiadanej informacji. Przeciwnie: obecność grawitacji sprawia, że stan entropii termicznej, w którym materia ma początkowo temperaturę T_CMB(p), jest stanem minimalnej w tych okolicznościach entropii, a siły grawitacji sprawiają, że materia zostaje zmuszona do ruchu (lub „stawania się”) w celu osiągnięcia stanu maksymalnej entropii, czyli w tym wypadku minimalnej informacji. W przywoływanym często w literaturze zamkniętym pudle materia w stanie równowagi termicznej, jakiej doświadcza na samym początku cyklu, przypomina raczej gaz o maksymalnym możliwym rozproszeniu cząstek, nieustannie zderzających się pod wpływem potężnej energii kinetycznej, uzyskanej w procesie pragmatropii, oczywiście kosztem posiadanej przed tym procesem energii potencjalnej. Średnia energia kinetyczna tego niby-gazu jest wyznacznikiem średniej temperatury tła kosmicznego na samym początku cyklu ewolucji. Będę oznaczał tę temperaturę symbolem T_CMB _(p) i odróżniał ją do temperatury tła na końcu cyklu, T_CMB(k), tuż przed uruchomieniem procedury kolejnej pragmatropii.

Dużo czasu zabrało mi zrozumienie i akceptacja odmienności naukowej entropii w warunkach obecności i nieobecności grawitacji. Rewolucję w mojej tradycyjnej wizji spowodował Roger Penrose dwoma swoimi dziełami: w przywoływanej tu kilkakrotnie „Drodze do Rzeczywistości”, ale także (i ostatecznie) w książce „Cykle czasu” (Prószyński i S-ka, Tłum. Bogumił Bieniok i Ewa Łokas). Warto zwrócić uwagę, że oryginał drugiej pozycji wydany przez The Bodley Head, London, ukazał się w 2010 roku. Sądzę, że mamy tu przykład niewątpliwej i godnej docenienia przez czytelników sprawności przekładowej i wydawniczej.

Proponuję w tym miejscu lektury spojrzeć na ilustrację 12-2 w tym podrozdziale. Wytłuszczone zdanie na poprzedniej stronie znaczy, że dla wartości α rekomendowanej przez CODATA stosunek T_P / T_CMB1(p) powinien być równy Φ^137,035⁹⁹⁹.

Aby uniknąć nieporozumień w dalszej części tekstu wprowadzę listę niezbędnych symboli:

T_P – temperatura Plancka, jednostka Plancka równa, jak już wyżej podałem, Φ^137,035 ⁹⁹⁹;

n – numer cyklu ewolucji Wszechświata. Jeżeli n wyraża się liczbą całkowitą, to n oznacza numer pełnego cyklu, a nie jego fazy. Przykładowo: jeśli n=5,661, to znaczy, że mamy na myśli i w komputerze zakończony już cykl nr 5 oraz jego część (fazę) 0,661;

T_CMB – temperatura promieniowania tła uformowanego według nauki ok. 400 tysięcy lat po Wielkim Wybuchu (w rozumieniu przestawionym w niniejszej opowieści, po eksflacji połączonych gwiazd bliźniaczych);

T_CMBn – temperatura promieniowania tła w cyklu n;

T_CMBn(p) – temperatura promieniowania tła na początku cyklu n;

T_CMBn(k) – temperatura promieniowania tła w ostatniej fazie cyklu n;

T_CNBCMBn(f) – temperatura promieniowania tła w fazie f cyklu n.

Wyprzedzając nieco dalszy tekst wprowadzę jeszcze dodatkowe potrzebne później symbole:

τ_n – długość czasu trwania cyklu n;

τ_n(fp) – długość czasu trwania cyklu n od początku do fazy f;

τ_n(fk) – długość czasu trwania cyklu n od jego fazy f do końca.

Posługując się symbolami możemy napisać:

Uparcie przypominam, że uogólnienie równania (12-2) przez równanie (12-3) jest wynikiem strat energii w procesie pragmatropii wynoszących Φ^-2 dla każdej pragmatropii o numerze większym lub równym 2.

Można pofantazjować i wyobrazić sobie scenariusz porcjowanego, „kwantowego” spalania masy Plancka w gwieździe bliźniaczej w ciągu jednego czasu Plancka, t_p=5,39121 x 10^-44s. będącego jedną z fundamentalnych jednostek systemu jednostek Plancka.

Tak więc wyobraźmy sobie, że paliwo pragmatropii podawane jest porcjami o podanej wyżej energii, podobnie do automatycznych podajników węgla w elektrowni, wskutek czego temperatura gwiazdy monotonicznie rośnie. Można pokusić się o ocenę czasu potrzebnego do osiągnięcia temperatury Plancka od „momentu”, w którym czoło fali intropii osiągnie umowną powierzchnię gwiazdy do momentu całkowitego spalenia zawartości zagiętego stożka z ilustracji 12-2, czyli całkowitego kolapsu. Piszę „umowną”, bo granica tej powierzchni jest rozmyta, podobnie, jak to jest w przypadku Słońca, gwiazdy o znacznie niższej temperaturze na powierzchni. Oszacowanie takie byłoby łatwe, gdyby znana była początkowa energia/masa protogwiazdy, ale nie jest znana. Niemniej jednak pokuszę się o oszacowanie energii/masy gwiazdy-matki naszego cyklu ewolucji, a także ocenę długości tego cyklu. Nie jest to zamierzonym wątkiem tej opowieści i dlatego zrobię to dopiero na końcu w formie aneksu.

Po tym przydługim wstępie powróćmy do mojej przygody ze stałą α. Jeżeli temperatura Plancka T_P jest najwyższą temperaturą pragmatropii na starcie np. do „naszego”, szóstego, cyklu ewolucji, to dobrze byłoby wiedzieć, jaka jest temperatura równowagi termicznej materii po zakończeniu pragmatropii. W tym celu wróćmy na chwilę do podrozdziału 8-2 i przypomnijmy wartości intropii termodynamicznej i informacyjnej, liczonej od początku pierwszego cyklu do aktualnej fazy „naszego”, szóstego cyklu:

A=11, 321 9245 (12-4)

B=A +3+Φ^-2 = 14,703 890 52 (12-5)

te wartości wykładników potęgowych liczby Φ będą zmniejszone o 10. Założyliśmy wcześniej, nie bez podstaw, że wzrost entropii termodynamicznej, towarzyszący każdej kolejnej pragmatropii następującej po pierwszym cyklu, wynosi Φ^2. Oznacza to, że każdy kolejny wszechświat rozpoczyna ewolucję z zasobem energii potencjalnej Φ^2-krotnie mniejszym niż jego poprzednik.

Będzie to bliżej wyjaśnione w podrozdziale 3.2.

Składniki intropii dla cyklu 6-go w fazie naszej kosmologicznej egzystencji, będą więc zmniejszone o 10, czyli:

A_0,661= 1,3219245, (12-6)

B_0,661 = 4,703 890 52 (12-7)

Przypomnijmy także średnią temperaturę mikrofalowego promieniowania tła według ostatnich pomiarów Plancka, w fazie „f” naszego, 5-go cyklu, która wynosi: T_CMB5(f) = 2,72548 K. Jaka jest ta faza, w której się znajdujemy obserwując Wszechświat?

Łatwo ją wyznaczyć: skoro pełny cykl ewolucji oznacza wzrost intropii termodynamicznej o Φ², to w naszej fazie wyniesie on Φ ^(A*/2), czyli Φ^0,661. I właśnie ta liczba, 0,661, jest w tej opowieści fazą naszego cyklu, którego numer, uwzględniający przebytą część równą 0,661, dokładnie wynosi 5,661. Żeby ułatwić pracę wyobraźni trzeba tu zwrócić uwagę, że „połowa” cyklu, którą w ziemskim systemie liczbowym zapisalibyśmy, jako ½ lub 0,5, w zapisie kosmologicznym wynosi Φ^-1 = 0,618033. Powołam się na geometrię „szkolną”: punkt na odcinku prostej wynikający z jego złotego podziału nadaje obu częściom tego odcinka szczególne właściwości. Stosunek dłuższego z odcinków do długości odcinka niepodzielonego oraz stosunek krótszego z odcinków do dłuższego (po podziale zwanym „złotym”) jest równy Φ^-1. Zgodnie z założeniami kosmicznego systemu liczbowego te proporcje powinny być przeniesione na odcinek spirali logarytmicznej.

Wynika stąd, że nasze położenie w cyklu 6 przekroczyło już jego „połowę”, ma za sobą etap ekspansji Wszechświata i znajduje się na etapie Wszechświata kurczącego się, niechybnie zmierzającego do kolapsu. Taki wszechświat nie jest więc ani nieustannie ekspandującym, ani nieustannie kurczącym się. Jest jednym i drugim, najpierw rozszerzającym się, a po przekroczeniu pewnego stanu kwantowego kurczącym się. Jak pogodzić ten drugi, bliski naszemu istnieniu stan, z prawem Hubble’a zostanie wyjaśnione w odrębnym podrozdziale.

Sądzę, że jest już usprawiedliwione duże znaczenie temperatury mikrofalowego promieniowania tła w tej opowieści. Przede wszystkim jest ona mierzalna w naszej fazie ewolucji Wszechświata, wprawdzie ogromnym kosztem, ale jednak, a ze zmierzonej wartości liczbowej można obliczyć z niezłą dokładnością wartości tego parametru dla dowolnej fazy dowolnego cyklu ewolucji. To wielki ukłon Wielkiego Kosmosu w naszą stronę: mierzcie moją temperaturę, a sporo dowiecie się o mnie, tak, jak mierząc temperaturę ciała człowieka lub ciepłokrwistego zwierzęcia można ocenić jego stan zdrowia (czyli równowagi termicznej albo jej braku).

Wyposażeni w taką wiedzę powróćmy do równania (12-3) i znając temperaturę Plancka oraz CMB w naszej fazie cyklu piątego spróbujmy obliczyć stałą struktury subtelnej dla początku cyklu 1-go.

Dane wyjściowe:

Obliczmy temperaturę promieniowania tła na początku cyklu 1-go. Skorzystamy (po raz pierwszy) z wartości intropii informacyjnej, która zawiera energetyczny odpowiednik informacji w odległej przeszłości, czyli po 1-ej pragmatropii. Dlaczego „informacyjnej”, a nie „termodynamicznej”? Dlatego, że wirtualna fala intropowa, startując ze stanu „teraz” do stanu z początku cyklu 1, musi zabrać ze sobą ładunek kontentu z fazy „teraz”, wbrew temu, że przejście przez co najmniej jeden horyzont informacyjny wymaga pozbycia się tego bagażu. Ta umyślona fala intropowa zachowuje się tak, jakby cofając się do początku cyklu 1-go nie było żadnego horyzontu. Czy to jest słuszne? Zobaczymy na ile to założenie jest prawdopodobne.

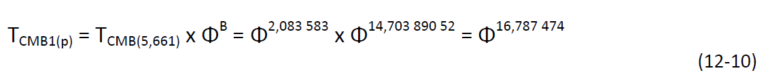
Teraz mamy już wszystko, żeby obliczyć:

No i mamy problem: pierwsza obliczona wartość (nie wykluczam następnych):

α_ob1(p) = 1 / 137,162 749 = 0,007 290 609, jest nieco mniejsza od „oficjalnej”, która wynosi:

α_CODATA₌0,007 297 352 566 4 ± 0,000 000 024. Pierwsza dotyczy początków cyklu 1-go, a druga? Nie wiadomo. Można tylko domniemywać, że dotyczy współczesnej nam fazy ewolucji Wszechświata w cyklu 5. A więc jest to „prawdziwa stała”, czy nie jest?

Stosunek tych wartości wynosi 0, 999 075 916 czyli (1,000 924 938)^-1. Odchyłka względna jest mniejsza od 0,1 %. Taka odchyłka może się wydawać mała i akceptowalna, ale nie w kosmologii, w której mamy do czynienia z wielkościami fizycznymi od 10^-44 do 10⁸⁸, nawet większymi. Wkrótce w tej opowieści spotkamy się z mnogością naukową, ocenianą na (10¹⁰)¹²³. A zatem nic dziwnego, że dużo czasu zużyłem na szukanie możliwego błędu obliczeniowego, wynikającego z ewentualnych błędów w publikacji danych, błędnego rozumowania i innych. Bezskutecznie. Chyba każdy czytelnik w tym miejscu pomyśli, albo podpowie: oczywiście chodzi o błąd „rozumowy”, niewłaściwe rozumienie danych wyjściowych. A zatem i ja, jako „czytelnik”, przyjrzałem się równaniu ( 12-1), definiującemu stałą α i skonfrontowałem to z kilkakrotnie wyrażanymi wątpliwościami, czy „szybkość światła w próżni c”, uznana przez świat naukowy jako uniwersalna, fundamentalna stała fizyczna, godna jest tego miana? Nie było wahania: to stała świetlna C₀ powinna zastąpić szybkość światła w próżni c („exact” według CODATA) w tych fundamentalnych prawach fizyki, w których jest to naukowo uzasadnione. Tak właśnie w moim głębokim przekonaniu jest w przypadku równania (12-1).

Nie należy utożsamiać szybkości dowolnego światła c ze stałą świetlną C₀, ponieważ nie ma takiego światła, które poruszałoby się z szybkością C_0. Przyznaję się jednak otwarcie, że nie do końca rozumiem znaczenie stałej świetlnej (jeżeli potwierdzi się jej istnienie) dla fizyki w szerokim znaczeniu.

Przejdźmy do rachunków:

C₀ = c x (1/ 0,999 075 915) = c x 1,000 924 938 = 300 069 747, 4 m/s (12-12)

C₀ – c = 277 289,4 m/s (12-13)

Wyżej podane wartości zapewniają zgodność obliczonej wartości α ze zmierzoną przez satelitę Planck temperaturą promieniowania tła.

Jestem przekonany, że w tym miejscu tekstu wytrwały czytelnik zapyta: czy to wszystko, co wyżej napisano oznacza podważenie, a być może nawet zaprzeczenie słuszności Szczególnej Teorii Względności? Na „pierwszy rzut oka” odpowiedź powinna brzmieć: tak! Jakkolwiek ta opowieść nie ma ambicji, żeby nazywać się „naukową”, to jednak nawet te zupełnie „nie naukowe” nie powinny sugerować czytelnikom wniosków wyprowadzonych „na pierwszy rzut oka”.

Zacznę więc od przypomnienia (por. podrozdział 2.1 z części II), że Albert Einstein, formułując swoją STW w kultowej już publikacji z 27 września 1905 r., a także w innych wcześniejszych i nieco późniejszych artykułach, nie przypisał stałej c konkretnej wartości liczbowej, ograniczając się do terminu „szybkość światła w próżni”. Jest jednak jeszcze druga kwestia: stałość szybkości światła. Najlepiej będzie, jeżeli zacytuję tu krótki fragment z dzieła profesora N. Davida Mermina w polskim tłumaczeniu profesora Jerzego Przystawy pt. „Czas na czas” (wyd. Prószyński i S-ka 2008):

„Mówi się, że szczególna teoria względności opiera się na dwóch zasadach: zasadzie względności i zasadzie stałości światła. W swojej znakomitej publikacji z roku 1905 Einstein nie użył słowa Pinzip w odniesieniu do tej drugiej zasady (jak to zrobił w odniesieniu do pierwszej). Zasadę tę scharakteryzował jako „postulat” (Voraussetzung). Postulował więc, że w pustej przestrzeni światło porusza się z prędkością, która nie zależy od prędkości ciała, które je wysyła. Takie sformułowanie jest równoznaczne z drugą zasadą, jeśli się je połączy z pierwszą, którą Einstein przedstawił jako postulat, iż pojęcie absolutnego spoczynku nie ma większego znaczenia w odniesieniu do zjawisk elektromagnetycznych, niż w odniesieniu do zjawisk zwykłej mechaniki Newtona.”

Wszystko to jest niewątpliwie bardzo interesujące, ale pozostaje pewien niedosyt: przecież nie chodzi tutaj o osobę i dobre imię Einsteina, bo On takiej osłony raczej nie potrzebuje, ale chodzi, mam nadzieję, o zbliżenie się do prawdy. Proponuję więc następujący scenariusz: przyjmijmy a priori, że postulat Einsteina jest godny doświadczalnego potwierdzenia. Wszakże żeby można było ten postulat nazwać teorią, powinien być falsyfikowalny. I może być poddany takiej procedurze. Wystarczy zainstalować na szybkim pojeździe źródło światła i, obserwując to światło na nieruchomym obiekcie w dostatecznie dużej odległości zmierzyć szybkość pojazdu, przy której strumień światła zostaje przerwany, albo pozostaje ciągły, nadal niewrażliwy na szybkość tego pojazdu.

Proste? Oczywiście. A zatem spróbujmy wybrać odpowiedni pojazd do testów. Przede wszystkim jakie szybkości powinien osiągać, żeby test był wiarygodny? Łatwo to określić na podstawie równania 12-13: ta szybkość powinna być równa co najmniej 277 289,4 m/s, czyli ok. 280 km/s. Czy to dużo?

Chyba tak. Zdaniem prof. Jerzego Przystawy („Odkryj smak fizyki”) taki pojazd narobiłby trochę kłopotów. Prędkość ucieczki potrzebna do wyniesienia pojazdu na orbitę okołoziemską wynosi 7,91 km/s, a prędkość ucieczki z Ziemi wynosi 11,2 km/s. Jeśli chcielibyśmy jednak (w co wątpię) wysłać ten pojazd poza Układ Słoneczny to musielibyśmy mu nadać prędkość ok. 1000 km/s, zaledwie trzykrotnie większą, niż wymaganą w teście. A więc falsyfikacja jest teoretycznie możliwa, praktycznie nie bardzo, bo nasz pojazd może nam umknąć. Oczywiście można by w teście użyć fali elektromagnetycznej o możliwie jak najmniejszej częstotliwości, ale wtedy pojawiają się z kolei kłopoty techniczne. A więc pozostaje nam wierzyć, albo nie wierzyć, w słuszność postulatu Einsteina i w zależności od tej wiary określać swój stosunek do STW. Autor tej baśni przyznaje, że nie widzi żadnych naukowych przesłanek, żeby fotony, cząstki, jak inne, miały zachowywać się w tak paradoksalny sposób, ale to jest problem autora, a nie Einsteina… Nie może być także poważnie traktowana i często powtarzana argumentacja na rzecz bezkrytycznego traktowania klasycznej STW, że przecież loty kosmiczne w dotychczasowym wykonaniu oraz GPS zapewniły wystarczającą, imponującą dokładność. Taka argumentacja nie przystoi w mediach nawet „bardzo popularnonaukowych”. Natomiast w kwestii akceptacji, a nawet nadużywania przez naukę słowa „exact” tam, gdzie są uzasadnione co do tego wątpliwości, zgody być nie może.

Właściwie niniejsza Opowieść w tym miejscu mogłaby się zakończyć: osiągnięty został jej główny cel, czyli odpowiedź na pytanie: czy wyobrażony Wszechświat może stanowić choćby częściowe wyjaśnienie wątpliwości albo paradoksów kosmologii naukowej? Jeśli można byłoby na to odpowiedzieć pozytywnie, zmieniając jedynie wartość liczbową jednej stałej fizycznej byłoby to, przyznaję, podejrzane, zbyt proste i łatwe. Wszechświat imponuje prostotą, ale nie do tego stopnia.

Potwierdza się to przez natychmiastowe pojawienie się nowej trudności: szybkość światła c wchodzi do wzorów definiujących co najmniej kilkanaście innych stałych, fundamentalnych dla całej fizyki. Czy stałą Plancka w równaniu (11-2) oraz stałą elektryczną w próżni ε₀ w tym samym wzorze można w tej sytuacji uznać za liczby pewne tzn. niezależne od szybkości światła w próżni c ? Stała ε₀ ma w CODATA atrybut „exact” (niestety czyni ją to „podejrzaną”), stała Plancka h w ciągu ostatnich15 lat przechodziła już różne korekty: od 6,626 068 96 x 10^-34 Js do 6,626 070 040 x 10^-34 Js. Nie są to różnice bez znaczenia. Również wartość intropii informacyjnej Φ^Bmoże budzić podejrzenie błędu, ponieważ stała sprzężenia B wynika z długości Plancka l_P, a ta jest związana ze stałą c i czasem Plancka t_P. Nasuwa się pytanie: która z tych trzech wartości jest naprawdę pewna? Jeszcze jednym paradoksem życia okazuje się, że najmniej pewna jest ta, która została opatrzona atrybutem „exact”.

Co można zrobić? Próba „korekty” stałych fizycznych byłaby z mojej strony desperackim i błędnym z założenia zamachem na dorobek fizyki w ciągu kilku pokoleń. Byłoby to również sprzeczne z intencją tej opowieści, która sprowadza się tylko do próby wzbudzenia ciekawości choćby jednego, otwartego na pomysły fizyka i, być może, zachętą do jakiejś kameralnej dyskusji. Naprawdę, tylko to. Ale niektórzy naukowcy zajmujący się stałością stałych także miewają podobne problemy. Oto jaką konstatacją kończą swój artykuł John D. Barrow i John K. Webb (patrz podrozdział 3.1):

… Dokąd doprowadziły nas zatem te gorączkowe poszukiwania zmienności α? Oczekujemy na nowe dane i nowe metody analizy tych zebranych już wcześniej w nadziei, że jednoznacznie potwierdzą zmienność α na uprzednio wykrytym poziomie lub jej zaprzeczą. Koncentrujemy się na badaniu stałej α, ponieważ konsekwencje jej zmienności dają się najłatwiej zaobserwować. Jeżeli jednak stała α jest zmienna, to inne stałe także powinny się zmieniać, i prawa rządzące naturą okażą się bardziej skomplikowane, niż zakładaliśmy w naszych najśmielszych wyobrażeniach.

Korzystając z właściwości nadanych w niniejszej opowieści pojęciu intropii, polegających m.in. na tym, że umożliwiają obliczenia parametrów Wszechświata w czasie „w tył” i „w przód”, kiedy znana i potwierdzona doświadczalnie jest wartość liczbowa jednego z nich (w fazie „teraz”), możemy pokusić się o wyjaśnienie problemu zmienności stałej α w czasie i w przestrzeni, zmienności wprawdzie znikomej, ale jak wynika z przytoczonego wyżej cytatu wielkich badaczy, dla astrofizyków niezwykle ważnej, przynajmniej póki nie zostanie naukowo wyjaśniona.

3. 4 Znikoma zmienność wartości liczbowej α. Wielki sukces astrofizyków doświadczalnych i ambitne wyzwanie dla teoretyków.

3. 5 „OPERA” w Gran Sasso (2011 r.) to może nie „finalna aria” „tragikomicznej opery”, ale raczej uwertura?

Nie roszczę sobie prawa autorskiego do tytułu tego podrozdziału. Jak wiadomo z tego, co napisano wcześniej (por. podrozdział 2.1 w części II), takimi określeniami, jak w cudzysłowach, opiniotwórczy polski tygodnik opatrzył dramat nauki i naukowców LNGS i CERN w publikacjach jednego z najwybitniejszych polskich fizyków akademickich. Przykre, ale prawdziwe.

Dlaczego więc z uporem powracam do tej smutnej i dla wielu osób prawdopodobnie kłopotliwej sprawy? Wydaje się, że w części II napisano już dostatecznie dużo.

Warto przypomnieć, że w świetle wszystkiego, co stanowi zasadniczą treść tej opowieści, neutrina w eksperymentach LNGS i CERN, zanim wyniki tych eksperymentów zostały przez liderów OPER-y zdyskredytowane, nie mogą być traktowane, jako „nadświetlne” (superluminous). Stosunek prawdopodobnej szybkości neutrin (299 799 782,4 m/s, por. podrozdziale 2.4) do zaproponowanej w podrozdziale 3.3 stałej świetlnej (300 069 747,4 m/s), jak łatwo sprawdzić, wynosi „zaledwie” 0, 9991, a więc o trzy lub cztery „dziewiątki” mniej, niż stosunek szybkości protonów do szybkości światła c w zderzaczu LHC w CERN. Nie może więc tu być mowy o złamaniu praw fizyki. Natomiast musi być niestety zgoda na stwierdzenie niezaprzeczalnego faktu, że przedstawiona tu argumentacja na rzecz poprawności albo błędności pierwotnych wniosków fizyków LNGS i CERN z marca 2011 r. jest przedmiotem rodem z wyobraźni, a nie rzetelnej dysertacji naukowej. To oczywiście zarzut bardzo poważny i właściwie spodziewać się można, że ta „trochę baśń” zostanie przez naukowców po prostu zignorowana, choć chciałoby się, żeby raczej bezpardonowo rozprawili się z autorem, gdyby tylko zechciał ją upublicznić.

No tak, ale „niestety” to nie wszystko, co każe zastanowić się nad problemem. Można sporządzić listę różnych innych wniosków, jakie zostały w tej pracy wywiedzione. Ta lista z konieczności nie będzie kompletna, bo problematyka jest tak szeroka, obejmująca tak rozległe domeny fizyki, że sam autor nie do końca panuje nad własnymi spostrzeżeniami i konstatacjami, nieraz przelotnymi. Autor sugeruje nieskromnie, że wymienione dalej wyniki obliczeń i wizualizacji graficznych mogą być choćby w części jeszcze jednym pomocnym wyjściem do prób logicznie spójnych odpowiedzi na ciągle rodzące się dylematy naukowe. Wymienię najbardziej niepokojące:

Czy interpretacja map CMB zmierzonych w ramach misji satelity Planck i zademonstrowanych publicznie w marcu 2013 r. istotnie nie podważa słuszności obowiązującego Modelu Kosmologicznego, znanego pod kryptonimem Lambda CDM, skoro zaprzeczają one tezie o jednorodności i izotropii Wszechświata? Przedstawiona tu koncepcja zdaje się dostatecznie obalać obecne opinie na ten temat.
Czym tłumaczyć swoiste zmilczanie lub niedocenianie naukowej wagi map CMB ukazujących obecność szumów promieniowania o temperaturze kilku μK, tworzącego charakterystyczne figury na nieboskłonie, które nazwałem w tej książce „szczelinami Plancka”? Można brzydko domniemywać, że wytłumaczeniem tego stanu jest po prostu niemożność pogodzenia ich z obowiązującym Modelem Kosmologicznym.
Czy stała struktury subtelnej α da się obliczyć z dużą dokładnością, nie wychodząc z wzoru Sommerfelda (podrozdz. 3.1, wzór 12-1), ale z całkowicie odmiennych danych wyjściowych i przy jednoczesnym nadaniu tej liczbie sensu fizycznego?
Czy jest możliwy uzasadniony wybór trajektorii w przestrzeni Wszechświata, wzdłuż której wartości liczbowe α, zmierzone przez kilka zespołów wybitnych eksperymentatorów świata z bardzo dużą dokładnością (co najmniej 10^-5), okazują się mierzalnie zmienne? Jakie może być tego wytłumaczenie?
Z jakich fizycznych przesłanek wynika to, że stosunek mas protonu i elektronu nie jest sprawą zwykłego przypadku, ale sam w sobie stanowi jeden z najważniejszych parametrów kosmologicznych?
Czy masa cząstki, np. neutrina, jest naprawdę stała, będąc współczynnikiem proporcjonalności między jej energią potencjalną i szybkością światła, czy też taka konstatacja jest zawodna, gdy szybkość tej cząstki jest porównywalna z szybkością światła i w dodatku podlega zmianom? Czy masa takiej cząstki (np. neutrina) może „oscylować” w trakcie jej ruchu i, jeśli tak, to dlaczego?
Czy jest zadowalające twierdzenie nauki, jakoby Wszechświat nieustannie się powiększał i że nie należy przewidywać kresu tego procesu innego, niż rozrzedzenie i rozpłynięcie się Wszechświata w otaczającej go hiperprzestrzeni? Jak pogodzić przedstawioną w tej opowieści koncepcję początkowej ekspansji, a następnie kurczenia się Wszechświata aż do pewnego określonego stanu, z obserwacjami astronomicznymi i z prawem Hubble’a? Jakie mogą być przyczyny zaobserwowanego przyśpieszenia „ekspansji” datującego się od ok. 5 miliardów lat?
Jaki jest powód przyśpieszonej rotacji materii na obrzeżach niektórych galaktyk spiralnych i gromad kulistych, nieobdarzony przez naukę przymiotnikiem „ciemny”, natomiast ewidentnie zaprzeczający newtonowskiemu prawu ciążenia powszechnego?

Na razie to wystarczy, sądzę, że w trakcie rozwijania tej baśni, będę mógł tę listę uzupełnić. Niektóre punkty (5, 6, 8) nie zostały jeszcze w tej pracy rozwinięte, bo wymagają wcześniejszych wyjaśnień, żeby mogły być przekonujące. Będzie na to miejsce w Części V i w Dodatku.

Wyobraźmy sobie jednak, że po tych dywagacjach niektórzy badacze postanowią powtórnie zastanowić się nad wymienionymi dylematami i że (jak marzyć, to marzyć) dojdą do wniosku, iż „coś jest w tej bajce na rzeczy”, nie bardzo jeszcze wiadomo co, ale jednak… I w takim wypadku, narzuca się oczywiste pytanie: czym naprawdę kierowali się liderzy programu OPERA w CERN i LNGS unicestwiając jednym komunikatem osiągnięte wyniki pomiarów? A jeśli okaże się, że pierwotne wyniki były przynajmniej „zastanawiające”, nawet po dokręceniu złącza światłowodowego, to jak ocenią ten fakt „etycy nauki”, jeśli tacy jeszcze w ogóle istnieją?

I to by było tyle, przynajmniej w sprawie Gran Sasso.