Część IV
Modelowanie Wszechświata
Spis treści podrozdziałów
Tytuły są podlinkowane. Wystarczy kliknąć, aby przenieść się bezpośrednio do wybranego podrozdziału.
4.1 Narodziny wielowszechświata cyklicznego.
4.2 Idea wielowszechświata cyklicznego. W którym jego cyklu my, Ziemianie, się znajdujemy?
4.3 Modelowanie Wszechświata zawierającego materię.
4.4 Rewelacje na mapach CMB z satelity Planck i ich ślady w przedstawionych modelach Wszechświata.
4. 1 Narodziny wielowszechświata cyklicznego.
W literaturze popularnonaukowej można spotkać różne konfiguracje „multiświata” cyklicznego, domniemywane przez autorów. Muszę ostrzec, że koncepcja, jaka będzie tu przedstawiona, bardzo odbiega od tych wcześniej opisanych gdzie indziej, jest bardziej złożona i wcale niełatwa do opisania, zwłaszcza że staram się w miarę możliwości unikać animacji obrazów, co przy lekturze może niekiedy nastręczać kłopoty techniczne. Na ilustracjach animowanych ruch zastąpiłby tekst. Zacznijmy od próby wyjaśnienia, jak mogło dojść do wyłonienia się w nadprzestrzeni gwiazd materialnych, dających początek całym konstelacjom? Częściowo zostało to wyjaśnione w rozdziale 3. W wyniku losowego łączenia się cząstek materii o grawitacji zarówno dodatniej, jak i ujemnej powstają olbrzymie (w znaczeniu kosmicznym) jej skupiska, które będziemy nazywać gwiazdami bliźniaczymi. Nazwa wynika stąd, że gwiazdy te, jeżeli już powstały, występują parami. Nie są jednakowe: są ze sobą nawzajem powiązane następującymi cechami:
- każda z nich zawiera po dwa rodzaje materii o ortogonalnych stygmatach czasu i o przeciwnych znakach grawitacji, są więc naznaczone odrębnymi duopolami, pokazanymi na rys. 3-1 B, (według innego możliwego scenariusza pierwotne gwiazdy bliźniacze były „monostygmatowe”, czyli występowały jako kwartety, a dopiero w następnej erze ewolucji stały się „duopolowe”, co uwzględniono na ilustracjach tego podrozdziału);
- masy wchodzące w skład obu gwiazd oraz gęstości tych mas są sobie równe;
- w każdej z nich, wskutek dużej gęstości masy, a więc małych odległości między cząstkami materii (o których nic nie wiemy), przeważa grawitacja dodatnia, a zatem oba obiekty się przyciągają;
- gwiazdy bliźniacze są wzajemnie kwantowo uwikłane (por. podrozdział 7.2 części I), co powoduje, że w trakcie ich kwantowego „stawania się” na trajektorii prowadzącej do połączenia pozostają takie same, zachowując wszakże odrębne stygmaty czasu i znaki grawitacji. Ponadto ma tu znaczenie siła wiążąca cząstki jednakowe pod względem masy, ale o przeciwnych znakach grawitacji, znane z podrozdziału 6.3 części I.
Trajektorie obu obiektów są oczywiście trójwymiarowymi spiralami logarytmicznymi o przeciwnych kierunkach zwijania, wymaga tego zakaz Pauliego (por. podrozdział 3.1 części 1). Z tego samego powodu, jeżeli wirują, to ich momenty obrotów, zarówno podstawowych jak i precesyjnych, powinny mieć przeciwne kierunki.
Na ilustracjach 12-1 A,B,C pokazano, jak gwiazdy bliźniacze zbliżają się do siebie, aby na końcu trajektorii spiralnych połączyć się, dając początek protogwieździe, a ta z kolei da początek wielowszechświatowi, w którym znajdzie się także Wszechświat, jaki obserwujemy i uważamy go za „nasz” (i słusznie).

Ilustracja 13-1 A. Narodziny pierwotnych gwiazd bliźniaczych w nadprzestrzeni. Faza uznana tutaj jako wstępna

Ilustracja 13-1 B. Narodziny i ewolucja pierwotnych gwiazd bliźniaczych w nadprzestrzeni. Faza pośrednia

Ilustracja 13-1 C. Narodziny i ewolucja pierwotnych gwiazd bliźniaczych w nadprzestrzeni. Faza końcowa, będąca zarazem narodzinami gwiazdy-matki pierwszego cyklu wielowszechświata
Pokazane wyżej ilustracje prowokują do dyskusji. Dlaczego obie sfery w trakcie ewolucji zmniejszają swoje wymiary? Powinny w zasadzie rosnąć, a nie maleć, bo w trakcie „podróży” przyłącza się do nich rozproszona materia o identycznych stygmatach i grawitacji. Taka możliwość wydaje się mało znacząca. W takim razie dlaczego maleją?
Patrząc z punktu fizyka klasycznego, zanim się zderzą w pobliżu centrów obu spiralnych trajektorii, znajdują się w stanach złożonego ruchu na odcinku spirali logarytmicznej, a także wirowania wokół tych odcinków. Kąt rozwarcia łuku każdego odcinka dla spirali „złotej” wynosi 25,7 stopnia. Sfery przestają być geometrycznymi sferami, wyginają się, wpadają w precesję i będąc w stanach immanentnego przyśpieszenia, tracą energię grawitacyjną. Objętość tych niby-sfer maleje jednak szybciej (Φ-3) niż rosną straty energetyczne (Φ2), a zatem gęstość energii/masy w każdym z obu obiektów rośnie Φ–krotnie. Spekulując dalej, mamy prawo przypuszczać, że finalne ich spotkanie zaowocuje potężną eksplozją. Będzie to eksplozja wymiarów powstałej w ten sposób nowej sfery, a nie rozproszenia materii w kosmos. Dlaczego? Pamiętajmy o dwóch rodzajach grawitacji oraz siłach utrzymujących cząstki o przeciwnych znakach tej grawitacji w „śmiertelnym” uścisku. Po osiągnięciu przez nowo powstały obiekt (który nazwę „protogwiazdą”) gęstości krytycznej nastąpi faza jego rozpadu na dwa sferoidalne obiekty, które powoli stygnąc, nabędą „ciała materialne” opisane już w rozdziale 1.7.1. części 1. Oba obiekty znacznie różnią się od gwiazd z ilustracji 12-1, przede wszystkim tym, że zawierają po cztery rodzaje materii, a nie po dwa. Ponadto żeby współistnieć na wspólnej trajektorii dalszej ewolucji, muszą spełniać warunek ortogonalności. Zostanie to pokazane w dalszej części niniejszego rozdziału.
W ten oto sposób weszliśmy w cykl pierwszy ewolucji Wszechświata.
4. 2 Idea wielowszechświata cyklicznego. W którym jego cyklu my, Ziemianie, się znajdujemy?
Na ilustracji 13-2 pokazano kluczowy moment ewolucji: narodziny Wszechświata cyklu pierwszego i jego gwiazdy-matki będącej przez to protogwiazdą całej rodziny wszechświatów, czyli wielowszechświata.
Ewolucja wielowszechświata odbywa się wzdłuż nielinearnej trajektorii, będącej spiralą logarytmiczną, rozciągającą się od promienia równego Φ–6 do promienia Φ+6. Założona, ale nie bezpodstawnie, dynamika ewolucji jednego cyklu jest więc równa Φ12. Zgodnie z tym, co zapowiedziałem w rozdziale 2, wszystkie konstrukcje graficzne będą oparte na czterech „cyfrach kosmicznych”: Φ, π, e i 1. Tam, gdzie okaże się to niemożliwe albo niecelowe, będę odstępstwo uzasadniał. To jest pierwsza ważna różnica tego opisu wobec spotykanych w literaturze. Na ogół ewolucję przedstawia się na linearnej osi czasu, której Wszechświat po prostu nie zna.

Ilustracja 13-2. Ewolucja wielowszechświata. Narodziny protogwiazdy i początek cyklu pierwszego
Protogwiazda pokazana jest w dwóch fazach, obie są skrajnymi postaciami z okresu „inflacji”, którą będę nazywać eksflacją, a którą z tej racji, że również podlega ewolucji, opiszę oddzielnie w dalszej części.
Protogwiazda dysponuje energią, która z założenia powinna wystarczać na istnienie i ewolucję całej pozostałej części wielowszechświata. Wraz z narodzinami gwiazdy-matki każdego następnego cyklu protogwiazda „znika”, jej energia zostaje przekazana następnemu cyklowi, ale nie całkowicie. Powstawanie każdego cyklu odbywa się poprzez eksflację (szybkie rozprzestrzenianie się) kolejnej gwiazdy-matki, lecz kosztuje to Φ-2 energii gwiazdy-matki poprzedniego cyklu. Realizuje się tu zasada pankosmiczna, zgodnie z którą przejście cząstki przez horyzont informacyjny do wewnątrz kosztuje Φ-1 (0,618) energii, wyjście z niego na zewnątrz dalsze Φ-1, a zatem dwukrotne „przebicie się” cząstki przez zamknięty horyzont informacyjny opłacone jest częścią Φ-2 (0,382) energii.
Tak to wygląda z „punktu widzenia” cząstki, która w drodze przemiany pragmy, czyli „pragmatropii”, usiłuje się znaleźć po drugiej tej przemiany stronie, czyli np. z kończącego się cyklu piątego do cyklu szóstego. Zapłaci za to 61,8% swojej dysponowanej energii. Takie same koszty pragmatropii zapłaci każdy kolejny cykl ewolucji wielowszechświata. Z naszych wcześniejszych obliczeń w podrozdziale 2.2 części II wynikają następujące aktualne wartości obu rodzajów intropii, liczone od początku cyklu pierwszego ewolucji wielowszechświata.
A=11, 321 9245
B=A +3+Φ-2 = 14,703 890 52
Tu dochodzimy do wniosku, że naszą fazę ewolucji poprzedziło 5 pełnych cykli oraz część cyklu szóstego, wyrażająca się intropią termodynamiczną, równą A-10 = 1,321 9245. Jesteśmy więc w szóstej odsłonie wielowszechświata, w fazie wyrażającej się częścią 1,321 9245/2=0,661 pełnego cyklu. Warto zapamiętać ten ułamek: 0,661, będzie dalej wielokrotnie przywoływany. Jeśli liczyć od początku cyklu pierwszego, to nasza faza w ewolucji Wszechświata wynosi 5,661, a do końca cyklu szóstego pozostaje nam tylko 0,339 jego części. W sposób raczej tylko poglądowy pokazano „naszą pozycję we Wszechświecie” na ilustracjach 13-2 – 13-4.
Cząstka przecinająca powierzchnię horyzontu nie może wnieść ze sobą do środka ani jednego bitu (albo czterobitu), całą informację o sobie musi pozostawić przed wtargnięciem do środka. Przypomina to żartobliwą ludową anegdotkę o Bramie Nieba: Tylko w koszulach przyjmujemy, tylko w koszulach, resztę proszę zostawić przed bramą, nic nie zginie. W tym niewinnym żarcie to, że nic nie zginie jest kosmologiczną prawdą!
Obniża się w ten sposób średnią intropię całkowitą i materia wychodząca z takiej przemiany jest znacznie bardziej uporządkowana, co wcale nie znaczy, że jej intropia termodynamiczna może być równa zero. Ten fakt musi zostać uwzględniony w graficznym modelowaniu Wszechświata. Jest oczywiste, że każdy cykl ewolucji nie ma żadnych możliwości przekazu informacji o cyklach, jakie już były i będą. Czyżby przypadek z długością Plancka (por. podrozdz. 8.2) był odstępstwem od tej reguły, jakąś „rozpaczliwą” próbą przekazu dla przyszłości? Pozostaje spekulować.
Pokazane ilustracje 13-2, 13-3 i 13-4 właściwie nie wnoszą nic nowego, ale pozwalają uniknąć animacji. Ale najważniejsze jest to, że żaden z tych rysunków nie wyjaśnia fundamentalnej kwestii: w jaki sposób kolejne cykle przechodzą z etapu ekspansji do etapu kurczenia się, zwanego często „etapem kolapsu”. Takie pytanie jest równoznaczne z pytaniem, w jaki sposób energia z cyklu n jest przekazywana do cyklu n+1. Po wielu próbach zrezygnowałem z prezentacji uwzględniającej zbyt wiele procedur jednocześnie, bo ilustracje te zatracają przejrzystość.
Żeby to pokazać, musimy odejść od szkieletowej budowy Wszechświata (patrz ilustracje 9-4, 9-5) i nadać mu… ciało, czyli materię, a dokładnie cztery rodzaje materii, które zostały wymienione i nazwane w podrozdziale 7.1. części I.
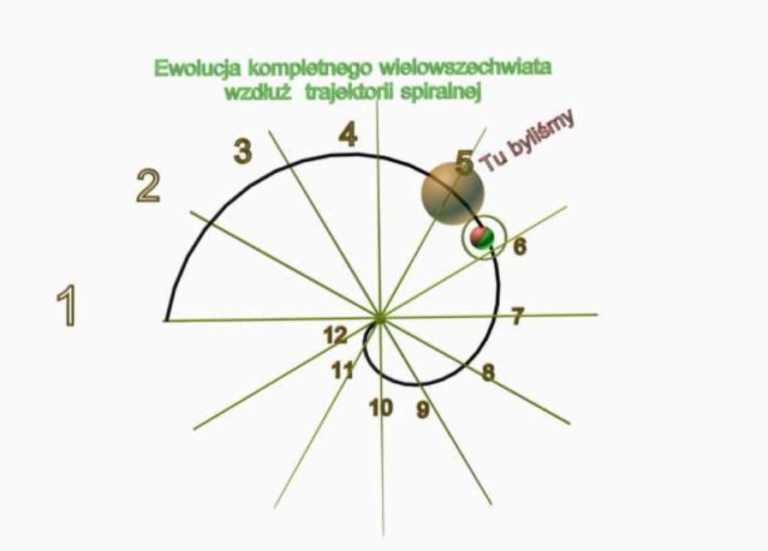
Ilustracja 13-3. Ewolucja Wszechświata. Początek cyklu piątego i domniemane nasze miejsce w tym cyklu

Ilustracja 13-4. Ewolucja wielowszechświata. Początek cyklu szóstego, a tuż przed nim domniemane nasze miejsce w cyklu piątym

Ilustracja 13-5. Ewolucja wielowszechświata. Początek cyklu siódmego.
4. 3 Modelowanie Wszechświata zawierającego materię.
Godzi się zacząć ten podrozdział od stwierdzenia, że modelowanie Wszechświata ma już swoją historię w nauce akademickiej. W rozdziale 3 części I przywołałem prace prof. Jerzego Jurkiewicza z Uniwersytetu Jagiellońskiego i jego współautorów z uniwersytetu w Utrechcie i Instytutu Nielsa Bohra w Kopenhadze. Jest także inny przykład takich przedsięwzięć z udziałem polskiego naukowca, Profesora Krzysztofa M. Górskiego (obecnie Jet Propulsion Laboratory, Pasadena, USA) zasłużonego w zaprojektowaniu systemu analizy przestrzeni o nazwie HEALPix dla misji satelity Planck. „Scientific American” („Świat Nauki”, luty, 2014) podaje m.in. taką wiadomość:
Kosmolog Yabebal Fantaye z University of Oslo wraz z Górskim i innymi badaczami przeprowadzili ostatnio 10 000 symulacji wyglądu CMB we wszechświatach, w których obowiązywał standardowy model ewolucji. Jak opisuje w artykule, który ukazał się w „Astrophysical Journal Letters”, obraz CMB przypominający naprawdę obserwowany pojawił się tylko w siedmiu wszechświatach testowych. Innymi słowy, standardowy model kosmologiczny tłumaczy obserwowane wyniki, ale ledwo ledwo.”
Nie mogę opisywać zastosowanej tutaj techniki grafiki 3D, która okazała się dla tej opowieści nieunikniona. Wystarczy, że wspomnę, że tzw. biblia kolejnej rocznej edycji programu liczy ponad 1400 cieniutkich stron, a dla osoby początkującej byłaby jeszcze przydatna druga biblia ze słownikiem terminów, stworzonych przez profesjonalnych grafików. Trochę przypomina to „język współczesnych matematyków”. Przyznaję się: zabrało mi to (z przerwami spowodowanymi zniechęceniem) niemal 10 lat nauki programu, jego licznych pułapek, a także wyszukiwania dróg postępowania, które by prowadziły do wyobrażonego lub poszukiwanego celu. Ogromne znaczenie przypisuję możliwościom animacji. W tej książeczce zamieszczam wiele ilustracji, których by tu nie było, gdybym miał pewność, że czytający radzi sobie ze ściąganiem plików AVI oraz ustawianiem ich optymalnych parametrów. Mam zamiar rozwiązać ten problem w nieodległej przyszłości, korzystając z aplikacji tzw. chmury, ponieważ większość pokazanych ilustracji ma swoje odpowiedniki animowane i byłoby szkodą ich zmarnowanie.
Przejdźmy więc od razu do modeli. Przedstawione tutaj i dalej modele nie są unikatowe, zostały arbitralnie wybrane spośród kilku zbiorów spełniających (jednak w różnym stopniu) wcześniej opisane warunki spójności opowiadanej hipotezy. Z jednym wyjątkiem: nigdzie nie było napisane, że ten hipotetyczny wszechświat musi być estetyczny, cokolwiek by przez ten przymiotnik rozumieć.
Teraz uzupełniam listę wymagań: model, wykonany graficznie lub inną techniką wizualną, bądź opisany słownie (co jest najtrudniejsze), albo równaniami matematycznymi, musi wywoływać pozytywne odczucia estetyki, a nawet piękna. Twierdzi się powszechnie, że nie ma piękna absolutnego, jest tylko subiektywne. Nie podzielam tego poglądu i upatruję w nim śladów powszechnej hipokryzji. Proszę o wsparcie matematyków, oni nie wzbraniają się nazywać niektóre równania „pięknymi” albo częściej „eleganckimi”. W literaturze popularnonaukowej ostatniej dekady można spotkać się z rozwiniętym uzasadnieniem tego poglądu. Mocne zdecydowanie w tej sprawie okazał Roger Penrose w Drodze do Rzeczywistości, o czym było wspomniane w rozdziale 3.
Przypomnę, że Wszechświat Sir Rogera obdarzony został trzema atrybutami: Prawda, Piękno i Moralność. A zatem i my, którzy czytamy tę opowieść, mamy prawo do sformułowania „swoich” atrybutów Wszechświata. Proszę pozwolić mi napisać o nich na końcu tej książki, najpierw sam muszę przyjrzeć się dokładnie temu, co zostało wcześniej napisane i zobrazowane.

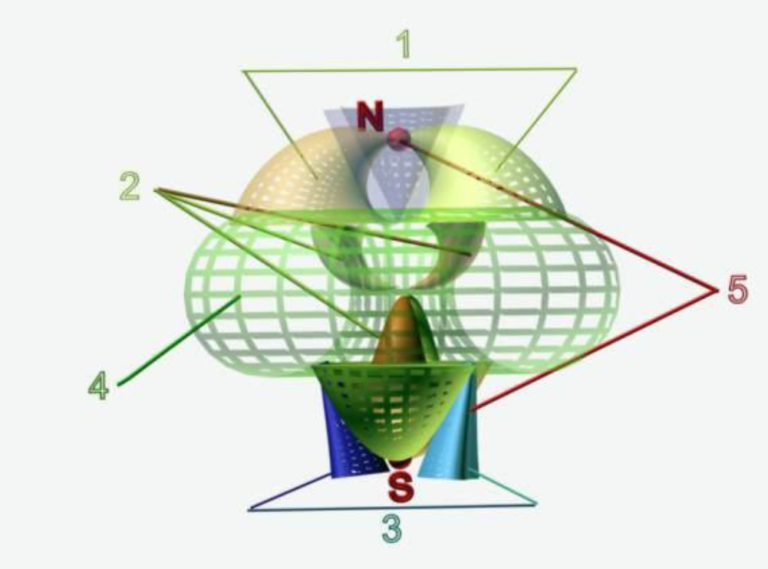
Ilustracja 13-6. Model realistyczny Wszechświata z materią w fazie szczytowej ekspansji następującej po fazie eksflacji. Na ilustracji nie pokazano jeszcze efektów skręcenia brył wokół półosi N(S) i centrum koła równikowego (por. 11-5)
Objaśnienia do ilustracji (tej i następnych):
- Materia „zwykła”, czyli koinomateria (np. jaśniejsza) oraz „antymateria” (np. ciemniejsza). Obie charakteryzują się grawitacją dodatnią i należą do grupy elksjomaterii. Ich stygmaty czasu są skierowane przeciwnie, zwrotami do środka układu.
- Materia jak w punkcie 1, ale znajdująca się jeszcze wewnątrz horyzontu ograniczającego przestrzeń w fazie eksflacji. Jak widać, przejście każdej z tych materii na drugą stronę horyzontu odbywa się kosztem utraty energii o czynnik Φ-1 i, w obecności pola grawitacyjnego, skutkuje też spadkiem intropii tych materii po przejściu przez horyzont, a więc zwiększeniem zasobu informacji, która opisuje jej stany kwantowe.
- Materia o ujemnej grawitacji, nazwana wcześniej sprochnomaterią, występująca w dwóch postaciach: z monopolami magnetycznymi N (np. ciemniejsza) i druga, z monopolami magnetycznymi S (np. jaśniejsza). Obie podlegają prawom traktrysy, opisanym obszernie w rozdziale 9. Figury niebieskie wyznaczają także przestrzenie o krzywiźnie ujemnej. Przekroje poprzeczne tych figur są wyznaczone przez dwie hiperbole różnego stopnia, czego poglądowy przykład jest pokazany na ilustracji 9-6.
- Torus będący horyzontem ewoluującej gwiazdy-matki (cyklu) w fazie, kiedy Wszechświat osiąga szczyt swojej ekspansji. W fazie „zerowej”, czyli narodzin tej gwiazdy, torus jest sferą o promieniu równym mniejszemu promieniowi rozwiniętego torusa. Torus płynnie przechodzi z postaci toroidalnej na sferoidalną przy zerowaniu większego promienia torusa. Płaszczyzna ortogonalnych osi torusa albo dwóch ortogonalnych promieni pochodnej sfery definiują płaszczyznę równikową Wszechświata oraz koło równikowe, obie wspólne dla obu jego połówek, N i S (wyjaśnienie niżej).
- Dwie bliźniacze gwiazdy, powstające tuż przed spotkaniem się „fal intropowych” koinomaterii i antymaterii w miejscach biegunów N i S, rozumianych dokładnie tak samo, jak na globusie szkolnym. Te gwiazdy, których zasoby energetyczne w dalszych fazach ewolucji ciągle rosną (bo przyciągają otaczające je materie, z których powstały), są najważniejszym akcentem hipotezy będącej treścią tej opowieści. Tak właśnie realizuje się przekazywanie energii gwiazdy-matki cyklu n-1 do mającego się urodzić cyklu n. W trakcie ewolucji cyklu oboje „bliźniacy” pod wpływem grawitacji zbliżają się do siebie, naśladując niemal dokładnie to, co robiły gwiazdy bliźniacze znane nam z ilustracji 13-1 A,B,C.
Patrząc na ilustrację 13-6 i jej następne wersje, trzeba pamiętać, że Wszechświat, taki jak powszechnie sobie wyobrażamy, nie jest „jednoczęściowy”. Składa się z dwóch na pozór identycznych półsferycznych wszechświatów oddzielonych od siebie torusem eksflacji. Nazwijmy je więc, aby uniknąć nieporozumień. Jeden, ten który znajduje się „na północ” od torusa, jako „Półwszechświat N”, i ten drugi, znajdujący się ”na południe” od torusa, jako „Półwszechświat S”. Wspólną podstawą dla obu półkul jest trzecia podstawowa część Wszechświata: przestrzeń torusa (na początku cyklu jest to sfera), z której w procesie nazwanym przeze mnie eksflacją następuje emisja wszystkich fal intropii, cztery do półsfery N i cztery do półsfery S, z zachowaniem wzajemnej ortogonalności tych fal.
W kosmologii naukowej pierwszy etap ewolucji Wszechświata nazywany jest inflacją.
Ilustracja 13-7. Model siatkowy Wszechświata z materią w fazie szczytowej ekspansji, następującej po fazie eksflacji. Tu i na dalszych ilustracjach, dla lepszej ich przejrzystości, nie pokazano jeszcze efektów skręcania brył wokół osi łączącej biegun N (lub S) z centrum koła równikowego.
Aby było to możliwe, posłużyłem się obrazami statycznymi. Nadal jednak będę musiał tak robić. Współuwikłanie kwantowe obu części Wszechświata zapewnia, że moment obrotowy całości jest zerowy, co oznacza, że mogą się one obracać lub być skręcane tylko w przeciwnych kierunkach. Oś obrotu N-S nie może wyróżniać jakiegokolwiek kierunku w nadprzestrzeni, dlatego wydaje się prawdopodobne, że wirujący Wszechświat doznaje także precesji o kącie odchylenia od osi ok. 90 stopni.
I jeszcze trzeba o czymś uprzedzić tych, których interesuje dalszy ciąg tej pasjonującej (mam nadzieję) opowieści.
Szanowni Państwo. To, co pokazano na ilustracjach podrozdziału 4.3 (powyżej), jest zaledwie wprowadzeniem do pełniejszego obrazu modelu Wszechświata. Jak wspomniałem wyżej, ilustracje animowane byłyby łatwiejsze w odbiorze ich treści, ale przekonalibyście się Państwo, że wobec niezwykle dynamicznej ewolucji wewnętrznej, o której napiszę dalej, byłyby po prostu mało przejrzyste. Dlatego tam, gdzie oddziaływanie na wyobraźnię czytającego będzie zależeć przede wszystkim od moich, bardzo niestety ograniczonych umiejętności graficznych, będę musiał posłużyć się większą ilością materiału graficznego, żeby pokazać nie tylko procesy, ale także ich fazy przejściowe.
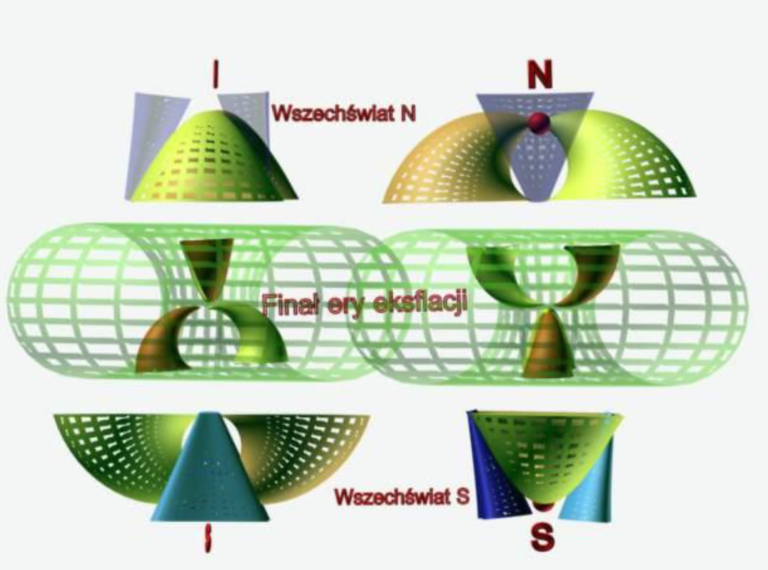
Ilustracja 13-8. Wszechświat z ilustracji 13-5 i 13-6 rozłożony dla celów poglądowych na wszechświaty składowe N i S oraz wspólną dla obu finałową fazę ery eksflacji. Pionowy zestaw po lewej stronie powstał z tego po prawej stronie przez obrót (nie mylić ze skręcaniem) o 90 stopni wokół półosi N(S) i centrum koła równikowego.
4. 4 Rewelacje na mapach CMB z satelity Planck
i ich ślady
w przedstawionych modelach Wszechświata.
Wszystkie materie po wypełnieniu przeznaczonych dla nich przestrzeni przekazują nam, obserwatorom z makroświata, bardzo istotne informacje. Nie wiedzielibyśmy o nich, gdyby nie misja ESA i satelity Planck. Czas więc przedstawić, co twórcy i badacze tego wspaniałego przedsięwzięcia zaprezentowali w 2013 roku szerokiej publiczności. Było to 6 lat temu, więc przypomnę obrazy lub ich fragmenty zademonstrowane wówczas przez ESA.
Ilustracja 13-9 jest mniej znana szerokiej publiczności. Została zademonstrowana na pamiętnej konferencji prasowej 21 marca 2013 r., jako mapa pokazująca zaskakujące „anomalie” w postaci „zimnych” i „gorących” regionów (The Planck data with hot and cold anomalies highlighted). Te „anomalie” w ewidentny sposób zaprzeczają twierdzeniom o jednorodności i izotropowości Wszechświata jako efektu ery inflacji, wylansowanej przez Allana Gutha.
Wszystkie mapy ESA z misji Planck przedstawiają rozkład promieniowania tła na całkowitej wewnętrznej powierzchni umyślonej sfery otaczającej miejsce ulokowania satelity, o promieniu równym największej odległości od satelity, przy której są jeszcze możliwości wykrycia obecności obiektów kosmicznych. Tak rozumianą sferę często nazywa się w literaturze sferą Wszechświata obserwowalnego.

Ilustracja 13-9. Jedna z map CMB w projekcji Mollweidego zademonstrowanych publicznie przez ESA 21.03.2013 roku.
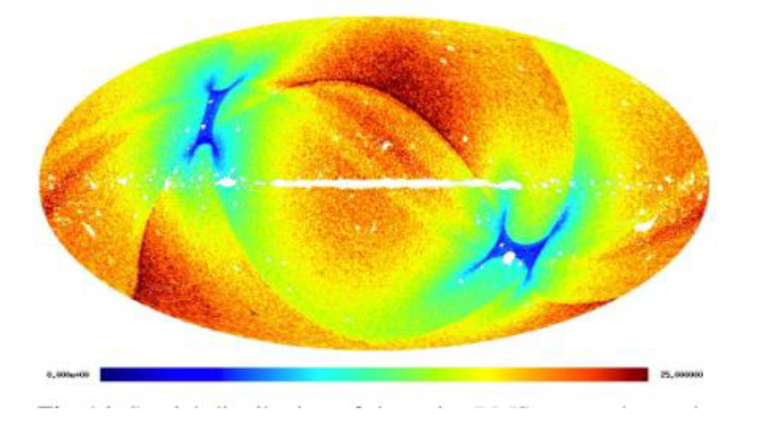
Ilustracja 13-10. Mapa rozkładu wartości skutecznej (RMS) szumów Gaussaowskich, przedstawiona za pomocą kolorów. Rozpiętość skali kolorów wynosi od zera (granat) do 25 mikrokelwinów (ciemne bordo)

Ilustracja 13-11. Mapa CMB uzyskana przez ESA w „misji nominalnej”. Kolory oznaczają wartości całkowitego czasu integracji pomiarów w granicach od 50 do 8000 sK-2

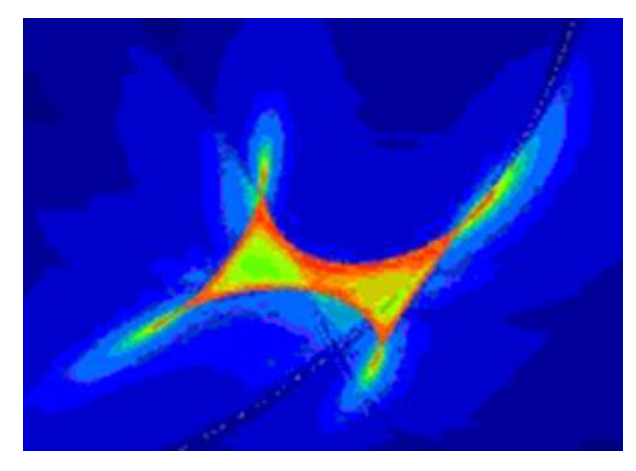
Ilustracja 13-12. Powiększenie „szczelin Plancka” z ilustracji 13-10 i 13-11 z zachowaniem ich kształtu i wzajemnego położenia kątowego. U góry: szczelina „równikowa’, na mapach ESA w północnej części elipsy Mollweidego. Niżej: szczelina „biegunowa”, na mapach CMB ESA w południowej części tej elipsy.

Ilustracja 13-13. Trzy główne części Wszechświata pokazanego wcześniej na ilustracji 13-7: pozostałość ery eksflacji (w środku), Wszechświaty bliźniacze (góra i dół). Obok pokazano przekroje poprzeczne, po obróceniu ich o 90 stopni. Właściwe położenie przekrojów pokazują poziome linie w kolorach takich, jak u przekrojów obróconych: równikowe w kolorze granatowym, biegunowe w kolorze czerwonym. Na tej ilustracji i następnych, 13-13 i 13-14, uwzględniono efekt skręcenia brył materii wokół półosi N i S o kąt 90 stopni.
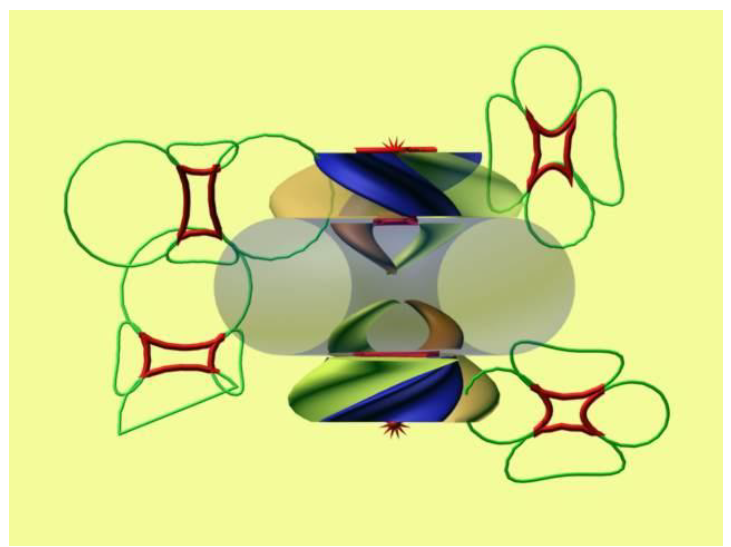
Ilustracja 13-14. Na przekrojach z ilustracji 13-12 zaznaczono czerwonym kolorem te ich fragmenty, które pochodzą z kolizji z materią zwykłą (koinomaterią), i dlatego emitowane stamtąd fotony mogą być odebrane przez aparaturę satelity Planck. Szczeliny są wypełnione plazmą o temperaturze rzędu miliardów K (patrz podrozdział 9.2)
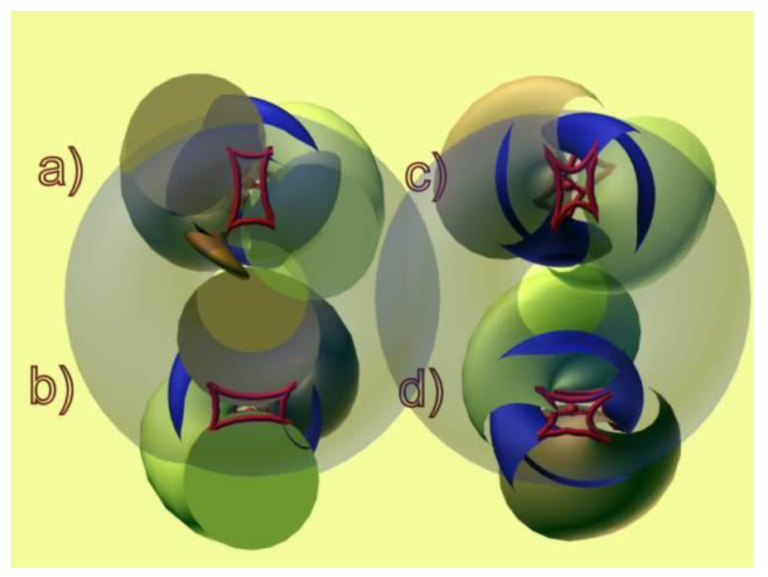
Ilustracja 13-15. Widok wszechświatów bliźniaczych: a) i b) od strony równika w kierunku biegunów, c) i d) od strony biegunów kierunku równika. Pokazano także otrzymane z prezentowanych modeli kształty szczelin Plancka (kolor czerwony), analogiczne do pokazanych na mapach ESA na ilustracjach 13-9, 13-10 i 13-11.
Ilustracje 13-12, 13-13 i 13-14 wraz z zamieszczonymi pod nimi objaśnieniami właściwie nie wymagają dodatkowych komentarzy. Jest wysoce zaskakujące, przynajmniej dla autora, że wyobrażony i raczej uproszczony graficznie model Wszechświata, pokazany na ilustracjach 13-6, 13-7 i 13-8, w tak dobitny sposób uświadamia, że ten model może prawidłowo odwzorowywać rzeczywistą strukturę obserwowalnego Wszechświata. Nie jest to zresztą jedyny argument na rzecz takiego przypuszczenia.
Wybrany dla misji Plancka sposób projekcji całkowitego nieboskłonu na elipsie o stosunku długości półosi równym 2 znany jest jako projekcja Mollweidego. Przy wielu zaletach tej projekcji w pomiarach CMB sprawia on niestety kłopoty, kiedy ma się do czynienia z innymi rodzajami układów współrzędnych. Nie można wtedy bezbłędnie porównywać takich map, natomiast transformacja projekcji wymaga specjalistycznego oprogramowania, często trudno dostępnego.